Potřebujeme-li, aby hloubka ostrosti sahala od jistého místa v popředí až do nekonečna, hodí se znát tzv. hyperfokální vzdálenost. Co to je a jak se používá, se dočtete zde. Naleznete tu i přehlednou tabulku hyperfokálních vzdáleností pro různá ohniska a clony a graf, který vám pomůže určit potřebnou clonu, víte-li, odkud chcete mít vše až do nekonečna ostré.
Při fotografování krajiny obvykle chceme, aby v záběru bylo vše ostré – jak popředí, tak pozadí. Pokud chceme do popředí umístit nějaký menší objekt (například květinu), musíme k němu být poměrně blízko, aby byl na fotografii dostatečně velký. Dosažení potřebné hloubky ostrosti pak může být problém. Jakou clonu nastavit? Kam zaostřit?
Selský rozum nám říká, že abychom plně využili pásmo ostrosti, které se nachází jak před, tak i za bodem, na který je zaostřeno, optimální je v takovém případě ostřit nikoli na pozadí nebo na popředí, ale někam mezi. Kam ale přesně? Odpověď zní: na hyperfokální vzdálenost. Co to je hyperfokální vzdálenost?
Hyperfokální vzdálenost se definuje jako vzdálenost, od které, když je objektiv zaostřen na nekonečno, je vše až do nekonečna ostré, čili přední hranice pásma ostrosti při zaostření na nekonečno. Tato vzdálenost závisí na ohniskové vzdálenosti objektivu, nastaveném clonovém čísle a v neposlední řadě také na tom, co ještě považujeme za ostré a co už ne.
Co ještě považujeme za ostré se vyjadřuje prostřednictvím průměru největšího akceptovatelného rozptylového kroužku. Pokud bod neleží přesně v rovině, na kterou je zaostřeno, zobrazí se na filmu nikoli jako bod, ale jako kroužek. Tomuto kroužku se říká rozptylový kroužek. Pokud je tento kroužek dostatečně malý, jeví se nám stále ještě jako přijatelně ostrý bod. K tomu, abychom mohli hovořit o hloubce ostrosti, hyperfokální vzdálenosti a pod., potřebujeme stanovit průměr největšího kroužku, který jsme ještě ochotni za bod považovat. Pro kinofilm se obvykle uvažuje největší akceptovatelný rozptylový kroužek o průměru 0,03mm. Tato hodnota se považuje za dostatečnou pro zvětšeniny až do rozměru 20x30cm. Pokud je objektiv vybavený stupnicí hloubky ostrosti, většinou je tato stupnice založená právě na této hodnotě. Pokud zvětšujete více nebo jednoduše jen máte zvýšené nároky na ostrost, můžete uvažovat největší akceptovatelný rozptylový kroužek o menším průměru, např. jen 0,025mm, jako je tomu u stupnic hloubky ostrosti objektivů Zeiss.
Známe-li ohniskovou vzdálenost f, clonové číslo N a průměr největšího akceptovatelného rozptylového kroužku c, můžeme hyperfokální vzdálenost spočíst podle vzorce
Proč zrovna tato vzdálenost je tou, na kterou chceme ostřit?
Pomocí hyperfokální vzdálenosti lze vyjádřit hloubku ostrosti při zaostření na danou vzdálenost. Označíme-li So vzdálenost, na kterou je zaostřeno, pak přední hranice pásma ostrosti je ve vzdálenosti
a zadní hranice
Zde, je-li jmenovatel záporný, zadní hranice je nekonečno. Odsud plyne, že nejmenší vzdálenost, na kterou když zaostříme, bude vše od přední hranice pásma ostrosti až do nekonečna ostré, je h+f. Přitom zaostříme-li na tuto vzdálenost, bude přední hranice pásma ostrosti (h+f)/2. Vzhledem k tomu, že ohnisková vzdálenost je obvykle v porovnání s hyperfokální vzdáleností zanedbatelně malá, tak v praxi platí, že:
Za starých dobrých časů, kdy existovala pouze pevná ohniska, mívaly objektivy stupnici hloubky ostrosti, kde byla hyperfokální vzdálenost vyznačená. Dnes už to ale není zvykem. Ostatně u zoomů to ani není prakticky proveditelné. Musíme si tedy poradit jinak. Pokud náš objektiv má stupnici hloubky ostrosti, hyperfokální vzdálenost snadno zjistíme tak, že zaostříme na nekonečno a na stupnici odečteme, kde je přední hranice hloubky ostrosti. Přesně tak je totiž hyperfokální vdálenost definovaná. Pak už zbývá pouze na tuto vzdálenost manuálně zaostřit a můžeme fotografovat. Pokud na objektivu stupnici hloubky ostrosti nemáme, nezbývá nám, než s sebou nosit kalkulačku či přehlednou tabulku hodnot pro různá ohniska a clony. Nebo si pro ohniska, která používáme, a pro pár clon budeme hodnoty pamatovat. Zde může být užitečné si všimnout, že hyperfokální vzdálenost je nepřímo úměrná clonovému číslu a tudíž, kolikrát se clonové číslo zvětší, tolikrát se hyperfokální vzdálenost zmenší. Vzhledem k tomu, že v posloupnosti celých clonových čísel je každé další vždy 1,4 násobkem předchozího, tak přivření clony o jedno číslo má za následek to, že se hyperfokální vzdálenost (a potažmo i hranice, odkud bude vše již ostré) zkrátí 1,4 krát.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabulka 1 – Hyperfokální vzdálenost (v metrech) pro běžná ohniska a clony. (Průměr maximálního akceptovatelného rozptylového kroužku 0,03mm.) |
V praxi ovšem obvykle máme opačný problém. Víme, odkud chceme mít vše až do nekonečna ostré, neboli víme,
kolik by měla být hyperfokální vzdálenost (dvojnásobek vzdálenosti této hranice) a kam ostřit. Co ale nevíme je, jakou potřebujeme nastavit clonu, aby vzdálenost, na kterou se chystáme zaostřit, byla
skutečně hyperfokální vzdáleností (a tudíž aby vše až do nekonečna bylo opravdu ostré). Potřebné clonové číslo zde je
kde d je námi požadovaná vzdálenost, kde už má být vše ostré.
Nemáme-li v kapse nebo v hlavě kalkulačku,
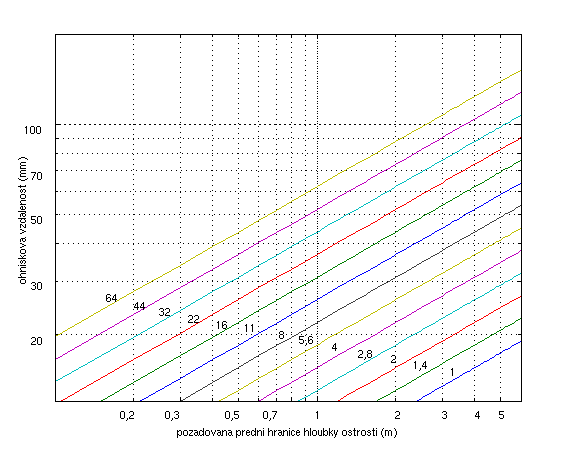
můžeme toto clonové číslo odhadnout buď prostřednictvím Tabulky 1 (v příslušném řádku najdeme nejmenší vzdálenost, která přesahuje dvojnásobek d, a v záhlaví sloupce odečteme nutnou clonu) nebo si můžeme vzít na pomoc graf na Obr. 1. V grafu vyhledáme bod, který odpovídá kombinaci použitého ohniska a požadované přední hranice pásma ostrosti. Clonové číslo pak zvolíme podle čáry nejblíže vlevo od tohoto bodu.
|
| Obr. 1 – Clona nutná pro požadovanou přední hranici pásma ostrosti při daném ohnisku. (Průměr maximálního akceptovatelného rozptylového kroužku 0,03mm.) V grafu vyhledáme bod, který odpovídá kombinaci použitého ohniska a požadované přední hranice pásma ostrosti. Clonové číslo pak zvolíme podle čáry nejblíže vlevo od tohoto bodu. |
Co dělat, když nám nevyhovuje průměr maximálního akceptovatelného kroužku 0,03mm? Stačí sí všimnout, že stejným faktorem, kterým vydělíme 0,03mm, musíme vynásobit clonové číslo. Například kroužek o průměru 0,021mm odpovídá posunu o jedno celé clonové číslo, protože 0,03 = 0,021/1,4 a vynásobení clonového čísla faktorem 1,4 přestavuje rozdíl právě jednoho clonového čísla. Pro takto velký kroužek můžeme hyperfokální vzdálenost snadno odečíst v Tabulce 1 – stačí se jednoduše vždy podívat o jeden sloupec dále vlevo. Stejně tak, oproti hodnotě clony vyčtené z grafu na Obr. 1, musíme o jedno číslo více zaclonit. Průměr kroužku 0,025mm, zmíněný výše, odpovídá rozdílu půl clonového čísla.
A ještě jedna rada na závěr, od paní profesorky. Pokud budete používat vzorce uvedené výše, nezapomeňte, že všechny vzdálenosti (včetně ohniskové!) je potřeba nejprve převést na stejné jednotky.

Pěkné, ale…
Článek se mi líbí je jasně a přeledně nastíněna problematika i její řešení. Někde jsem ale četl, že když např. fotím hory, kde skutečně hlavní motiv jsou horské masivy (tedy objekty v nekonečnu), pak je lepší zaostřit na ty hory a oželet rozmazané popředí, než se snažit zaostřit na hyperfokální vzdálenost a tím pádem nemít “ostré” ani popředí ani hory vzadu.(To nemít ostré v uvozovkách je samozřejmě s nadsázkou). Chápu to, zě to ve skutečnosti bude ostré, ale tak, že akceptuji právě ten rozptylový kroužek. Moje otázka tedy zní: je tato ůvaha správná. Není zaostřování na hyperfokální vzdálenost užitečné hlavně pro reportáže?
Jak fotit např. ty výše zmíněné hory, když chci, aby ty hory byly to, co přitáhne pozornost. Nebavme se o 10×15, ale o 30×40 a víc. Díky za odpověď. Petr.
RE: Pěkné, ale…
Podle me v tomto smeru nejde stanovit zadne univerzalni pravidlo. Zalezi na prilis mnoha faktorech – jak blizko jsou objekty v popredi, jak jsou vyrazne, jak moc se snimek nakonec zvetsi atd. atd.
RE: Pěkné, ale…
Nejsem sice zadny odbornik, ale zrejme jsem nejak nepochopil myslenku tvoji otazky. Pote co jsem si peclive precetl o jevu “hyperfokalni vzdalenost“, myslim ze jsi nepochopil podstatu.
Pises:
…než se snažit zaostřit na hyperfokální vzdálenost a tím pádem nemít “ostré” ani popředí ani hory vzadu.
Jeste jedna citace ze “starsiho” Paladixu:
Zajímavým jevem je tzv. hyperfokální vzdálenost. Při zaostření na tuto vzdálenost leží zadní hranice hloubky ostrosti právě v nekonečnu a hloubka ostrosti má maximální velikost.
Tak tedy:
pokud budes mit objektiv zaostreny na hyperfokalni vzdalenost (popripade dal), bude zadni hranice hloubky ostrosti v nekonecnu. Potom nechapu, proc by jsi nemel mit “ostre” hory vzadu. Otazka je spise v tom “kde bude predni hranice hloubky ostrosti”, aby jsi nemel rozmazane popredi. To je uz otazka volby clony nebo vhodnejsiho objektivu. Takze pokud mas pocit, ze hory vzady jsou neostre, podle me nemas zaostreno na hyperfokalni vzdalenost.
RE: RE: Pěkné, ale…
Ono jde vlastne o to, ze neni hyperfokalni vzdalenost jako hyperfokalni vzdalenost. Pokud vezmete tu pro standardni krouzek, a udelate obrovskou zvetseninu, tak hory budou neostre, protoze pro takove zvetseni je standardni krouzek prilis velky. Tzn. mela by se pouzit jina hyperfokalni vzdalenost, pro mensi krouzek, jenze a) ta vzdalenost muze byt uz hodne velka, takze stejne musime nakonec nechat neco neostre, nebo b) ani nevime predem, na jak velke plachty budeme zvetsovat a jaky krouzek a potazmo hyperfokalni vzdalenost bychom vubec meli pouzit. V takove situaci, pokud hory vzadu jsou hlavni subjekt, na kterem zalezi, tak opravdu muze byt nekdy rozumne si zivot zjednodusit, na hyperfokalni vzdalenost se vykaslat a ostrit na ne.
RE: Pěkné, ale…
Ted se musim trosku zastydet a dopsat dodatek. Sam jsem si poradne neprecetl tvoji otazku a spise jsem poucoval, nez bych odpovedel “k veci”.
Ted je mi jasne ze chapes ze to ve skutecnosti bude ostre, tak ze se akceptuje rozptylovy krouzek. Nevim jakou mas pod timto pojmem predstavu, ale podle me to spise souvisi s meznim rozlisenim filmu. Dobre by se to vysvetlovalo na digitalni fotografii, kde si misto rozptyloveho krouzku predstavime pixel (tedy obrazovy element). Prave diky tomuto “konecnemu” prvku, ktery zaznamena uplne stejne bod, tak i maly krouzek (pokud ten krouzek bude “mensi” jako samotna svetlocitlivy bunka odpovidajici pixelu), existuje urcite pasmo neostrosti, kteremu se neformalne rika hloubka ostrosti. “Teoreticky” vsechny snimky v tomto pasmu budou stejne a okem nerozeznatelne. U filmu je to podobne, ale slozitejsi. Navic, ne jenom film, ale i cocka ma mezni rozliseni, kdy bod promitne na film jako krouzek o malem prumeru.
U filmu navic existuje jev, ktery je neprijemny. A to je hrubnuti zrna. Cim je film citlivejsi, tim vice hrubnutim zrna trpi (nadruhou stranu neni potreba tak dlouhych expozicnich casu). Jak bylo receno, cim je vetsi clona, tim se hloubka ostrosti zvetsuje, jenomze tim je potreba delsi cas expozice. U citlivych filmu je pri velkych expozicnich casech hrubnuti zrna velice dobre okem pozorovatelne. Jeste stoji za zminku, ze pri velke clone (tedy male dirce) vznika tzv. difrakce (proto nejde zvetsovat clonu do nekonecna). Tyto vsechny jevy jdou proti sobe.
Jak rekla Radka, je dost obtizne dat presny recept a zalezi na mnoha faktorech. Podle me, pokud chces delat krajinky (jako staticke snimky) a z nich velike fotky (30×40 a vice), chce to vzit malo citlivy film (100 a treba i 50), stativ a hodne clonit (dlouhe expozicni casy). Fotka bude potom pekne ostra a bez znacne hrubych zrn. Ale zrejmme zalezi na zkusenosti a leckdo bude mit jiny nazor.
Hyperfokalni vzdalenost
V clanku zaznela skutecne pravdiva slova – Za starych dobrych casu, kdy hloubka ostrosti byla vyznacena na objektivu… Tady je kamen urazu, ze na vetsine beznych dnesnich fotacich jsou ruzne pitominky (kreativni programy, displeje atd.), ale tato zasadni vec tam neni (napr. Nikon F60, Canon 3000 aj. a to za vice nez 10000 Kc!). A proto drzitele techto zazraku, pokud chteji mit bud hory a kytky ostre nebo jen cast mit ostrou -/coz je pochopitelne nutne pro dosazeni autorova zameru, co chce potlacit nebo zvyraznit/ – museji mit s sebou graf nebo vzorecek z vyse uvedeneho clanku. A namisto aby tvorili, tak pocitaji, pletou se a dilem vyhazuji svou praci do kose. Vzpomenu-li i lacine fotaky (Flexaret), ze takto byly vybaveny!!!
RE: Hyperfokalni vzdalenost
Tady je kamen urazu, ze na vetsine beznych dnesnich fotacich jsou ruzne pitominky (kreativni programy, displeje atd.), ale tato zasadni vec tam neni (napr. Nikon F60, Canon 3000 aj. a to za vice nez 10000 Kc!).
Kamen urazu neni ve fotoaparatech, ale objektivech, jak ostatne autorka uvadi v textu. Jak na Nikon F60, tak Canon 3000 si muzete koupit pevne ohnisko, obvykle levnejsi a lehci nez zoom, i s hyperfokalní skalou.
RE: RE: Hyperfokalni vzdalenost
To je pravda, omlouvam se za nepresnost. Hloubka ostrosti je skutecne vyznacena prevazne na objektivech a ne na fotacich (na telech). Ale pak si asi musite takovy objektiv zrejme prikoupit (standartne se nedodava), no ale pak takova hloubka ostrosti muze prijit i na dalsi pekne penize….
Hyperfokální vzdálenost (pro Jardu)
S cenou tech monofokalu to neni zas az takova hruza, pokud se nekupuji nove. Ja mam na sveho pentaxe 3 (z toho 2 original pentax) za cenu velmi podprumerneho setoveho zoomu. Chce se to porozhlidnout po bazarech a mit stastnou ruku.
RE: Hyperfokální vzdálenost (pro Jardu)
Mily Vajco,
reseni muze byt vpodstate dokonce jeste lacinejsi nez to, co navrhujes. Tady v Paladixu existuje napad v clanku – Stupnice vzdálenosti pro objektiv Canon 50 mm/1,8 II – kde je popsano, jak lze na objektiv prilepit stupnici v metrech ( z papiru) a tim resit hloubku ostrosti.
Tady ale myslim si konci veskera sranda, tohle mi uz pripomina kompletni totac v plne parade! Neco jako: Urob si sam a nechod do Tuzexu.
začátečník
Jsem teprve začátečník. Fotím asi teprve dva roky se zrcadlovkou a hrozně mě to baví. Nikdy jsem si nemyslel, že budu schopen do nějakého koníčku, kterých mám pochopitelně víc nacpat takové peníze jako do focení. Ale jestli je ve fotografování více takových záležitostí jakou je výše uvedená Hyperfokální vzdálenost, tak se bojím abych s focením předčasně nepřestal. Mám docela obyčejné středoškolské vzdělání a matika mi nikdy moc dobře nešla a obávám se, že takovéto technologické postupy nejsem schopen pobrat ani z monitoru. Už chápu, že na fotogrfii je potřeba zvláštní studium, které vzhledem k rodiným povinnostem ani věku :-))) asi nikdy neabsolvuji. Nyní když pozoruji výsledky jiných amatérů, nebo čtu takovéto články (po kterých jsem mimo jiné do teď usilovně pátral, poněvadž na pultech knihkupectví jsem nalezl pouze literaturu, kde mi poradí co si mohu koupit abych dosahoval dobrých výsledků, ale nikde ani zmíka o tom jak vlastně na to), začínám si coby fotograf připadat méněceně či spíše zakomplexovaný jedinec, který čím víc začíná do problematiky fotografování pronikat, tím s větší hrůzou v mysli zjišťuje, že o focení vlastně neví vůbec nic! A přestávám pomalu věřit tomu, že by se ty kýžené výsledky díky mé tumpachovosti mohly někdy v budoucnu vůbec dostavit. Jinak díky za tento článek a doufám, že mi morálka dovolí podobné jěště vyhledat :o)
RE: začátečník
Neviděl bych to tak dramaticky. Já tedy fotím jen s pevným sklem. Takže tam tu stupnici mám, ale stejně ji ‘nevěřím na 100’ a zaostření přizpůsobím dle požadavku v konkrétní situaci. Myslím, že okopírovaná tabulka z článku pro orientaci bohatě postačí. Trochu bych to přirovnal k volbě expozice. Jsou tu dnes možnosti automatického nastavení expozice dle času, clony, kreativní programy apod. Když vzpomenu dědu který sice chodil s expozimetrem, ale nikdy jsem ho neviděl ho použít, tak nějaký komplexy jdou stranou. A fotky měl krásný. A to nemluvím když jsem ho viděl ‘čarovat’ pod zvětšovákem. Obecně bych řekl, že když to vezmeš zhruba dle tabulky a dáš tomu ránu jistoty(clona or vzdálenost), tak se max. dostaneš na menší bod, než je standart. A to nevadí. Další cestu bych viděl v onom nepopulárním archivování okolností(clona, focus, čas atd) fotek, pak lze fotit téměř s jistotou.
Navíc když je s velkou clonou ostření na nekonečno třeba 8m tak ta dolní hranice(resp. posun) se pohybuje už u centimetrů. Takže když zaostřím o metr dále, tak se mi dolní konec posune jen o 10 cm. Což se většinou dá vyřešit změnou pozice apod.
RE: začátečník
Klidek. Ta matika je potreba jen u takovych zbesilosti, jako mam treba ja, canon eos 500, ktery maj kontrolu hlkoubky ostrosti nepouzitelnou. Kazdej jinej fotak ma budto stupnici na objektivu, nebo pouzitelnej program nastaveni a kontroly hloubky ostrosti. Mimoto, po par zmrsenejch fotkach to clovek zacne celkem bezpecne odhadovat.
RE: začátečník
jsem jeste vic na zacatku nez Ty, fotim teprve rok a fakt se zatim jen ucim :))
kazdopadne me (a verim ze i profesionalum) hodne pomohlo “kolecko” http://dfleming.ameranet.com/ – doporucuju, da se nastavit presne podle vaseho objektivu, da se udelat tabulka hyperfokalnich vzdalenosti v zavislosti na clone a ohniskove vzdalenosti vcetne hloubky ostrosti popredi (jinymi slovy odkud budu mit obraz ostry pri zaostreni na hyperfokalni vzdalenost…)
jen abyste nehledali Circle of confusion: pro 35mm kinofilm je to 0.030, pro digital 0.008
Predvolba hloubky ostrosti u Canonu
Skvely clanek,jen bych pridal ze nektere aparaty Canon maji funkci, kdy si dvojim namacnutim spouste vymezite hloubku ostrosti a pri tretim [po zaverecne kompozici] neudela nic jineho ,nez ze propocita potrebnou hyperfokalni vzdalenost a zaostri prave tam kam je treba.Netusim sice jaky rozptylovy krouzek bere program v potaz a nikde to neni ani uvedeno,ale myslim ze pri pouzivani zoomu je to vcelku uzitecna vec.
tiez zaciatocnik
Kedze fotim iba pol roka tak sa povazujem za amatera – zaciatocnika. Nic ale nevidim tak tragicky ako dakto iny, prave naopak, tento clanok ma podnietil v experimentovani lebo ako vieme najlepsie sa clovek uci z vlastnych chyb a aj som trochu rad ze som o tejto stranke pred pol rokom nevedel. Pred precitanim tohoto clanku som mal aku taku znalost o hyperofokalnej vzdialenosti a co to je a robi, ale nebolo mi uplne jasno ako sa k nej dopracovat. Preto povazujem tento clanok za opravdu vyborny a ked mu niekto nerozumie nech sa netrapi, nestoji to za to. Moj zaujem bol urcite podnieteny aj tym, ze sa zaujimam o techniku a to sa odraza aj v tom, ze najradsej chcem manualny fotak, poloautomaty s priradenim clony nemam rad. Preto radsej fotim na Zenit EM ako na Prakticu B100. Ale tam uz su rozdiely naozaj velmi velke, najma optika tej Praktiky je neporovnatelne lepsia (objektivy). Preto sa snazim zohnat si B200, BX 20 je moc draha, nakolko som vojak na civilnej sluzbe a dostavam mesacne smiesnych 700 Sk to mozem zabudnut. K tomu si treba pripocitat naklady na filmy, vyvolanie, fotky, etc…
vypocet hyperfokalni vzdalenosti on-line
http://www.photozone.de/3Technology/demos/depth.htm
teda huraaa
Hurraaa konecne som to pochopil. Teda zabralo mi to nejaku tu chvilku ale myslim ze som tomu pochopil. Uz aj utekam si tuto novu vedomost odskusat v praxi…
Vdaka za cenne rady.
Milan
otázka
Dobrý den, mám možná hloupý dotaz. Nějak mi z článku nevyplynulo, zda tabulka hyperfokálních vzdáleností počítá s FYZICKÝM nebo EKVIVALENTNÍM 35mm ohniskem (tedy přepočet u dSLR). Může někdo poradit? Díky.
otázka
Zřejmě otázka ještě nebyla zodpovězena, proto si na ní dovolím reagovat. V celém článku se hohoří také o rozptylovém kroužku. V tabulce je velikost tohoto kroužku uvedena také. Tato tabulka je tedy platná pro ten rozměr negativu/ čipu, pro který je uvažován tento rozměr rozptzlového kroužku. J.
Tabulka krouzku
Tabulka pro různé foťáky
http://www.dofmaster.com/digital_coc.html#coccalculator
Hyperfokální vzdálenost
Našel jsem tabulku pro Hyperfokální vzdálenost,kam si můžete dosadit jakékoli údaje a ono Vám to přepočítá hodnoty.http://www.photozone.de/3Technology/demos/depth.htm
Tak snad to někomu pomůže.Zdraví Pavel
vzdalenost
“Co ale nevíme je, jakou potřebujeme nastavit clonu, aby vzdálenost, na kterou se chystáme zaostřit, byla skutečně hyperfokální vzdáleností (a tudíž aby vše až do nekonečna bylo opravdu ostré).”
A jak zjistíme, jak velká je vzdálenost, na kterou se chystáme ostřit?