Ještě jednou se zde vracíme k článku, který Ondřej Neff loni uveřejnil na DigiNeffu a kolem kterého se strhnula na FotoPrůvodci rozsáhlá diskuse.
V minulém dílu seriálu o čudlíkování jsem se dost podrobně zabývala převzorkováním obrázků. Pokusila jsem se tam mimo jiné vysvětlit, co je to interpolace a jak funguje, a zmínila jsem se tam též o tzv. Nyquistově frekvenci. Ráda bych toho teď využila a ještě se vrátila k tématu, o kterém se před časem na FotoPrůvodci velmi bouřlivě diskutovalo. Chci zde ukázat, že to, co Ondřej Neff napsal ve svém článku Co je CCD (5) uveřejněném na DigiNeffu, je chybné a že pravda je ve skutečnosti na straně čtenáře, kterého Ondřej Neff obvinil ze základního nepochopení principu generování digitálního obrazu.
Sensor digitálního fotoaparátu tvoří pole světlocitlivých buněk. Dopadne-li na buňku světlo, vytvoří se na ní elektrický náboj, jehož velikost je úměrná množství světla, které na buňku dopadne. Velikost náboje se pak převede na číslo, které reprezentuje intenzitu obrazu v daném bodě. Problém ale je, co s barvou. Každá buňka totiž generuje jen jednu hodnotu intenzity a my, abychom zachytili barvu, potřebujeme tři – pro každý ze tří barevných kanálů jednu.
V případě skeneru, kde se obrázek snímá postupně po řadách, lze jednoduše v každém bodě provést měření tři. Buď lze použít jednu řadu buněk a provést expozici třikrát, pokaždé světlem jiné barvy, nebo se snímač může skládat ze tří řad buněk, každé citlivé na jinou barvu, a tím, že se snímač posune vždy jen o jednu řadu, se v každém bodě postupně změří intenzita pro všechny tři barevné kanály. Při fotografování si takový luxus ovšem bohužel obvykle nemůžeme dovolit. Pokud by se scéna exponovala takto postupně, bylo by to příliš pomalé a v průběhu snímání by docházelo ke změnám scény a polohy fotoaparátu, což by mělo za následek nežádoucí deformace obrazu. Proto je potřeba expozici provést najednou. Nejběžnějším způsobem řešení problému barvy je použití obdélníkového pole buněk, kde každá buňka má před sebou barevný filtr a je tudíž citlivá pouze světlo jisté barvy (CFA – Color Filter Array). Obdržíme tak současně hodnoty intenzity všech kanálů, nicméně, protože se expozice provádí najednou, máme pro každý kanál hodnoty v jiných bodech.
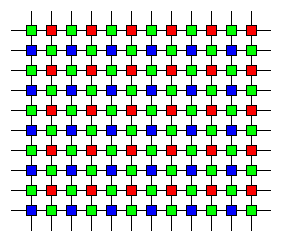 |
| Obr. 1 – Uspřádání buněk sensoru |
Buňky ciltivé na jednotlivé barvy mohou být rozmístěny různě. Nejoblíbenější je Bayerovo uspořádání zachycené na Obr. 1. Každá čtveřice sousedních buněk zde obsahuje dvě zelené buňky, jednu červenou a jednu modrou. Zelené buňky jsou umístěné na jedné diagonále, červená a modrá buňka na opačné.
Počet pixelů výsledného obrázku bývá stejný jako počet buněk, až na pár extra řad buněk po stranách potřebných při interpolaci. Pozice pixelů jsou stejné jako pozice buněk, v každém bodě ale známe hodnotu jen jednoho kanálu. Pro zbylé dva kanály ji musíme doplnit. Jinými slovy, známe hodnoty kanálů na sítích bodů zobrazených na Obr. 2 a potřebujeme dointerpolovat jejich hodnoty ve všech ostatních bodech, kde se přímky protínají, t.j. na sítích znázorněných na Obr. 3.
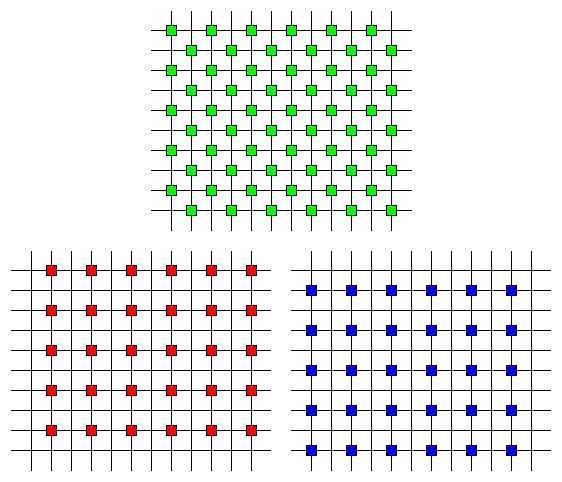 |
| Obr. 2 – Vzorky barevných kanálů před interpolací |
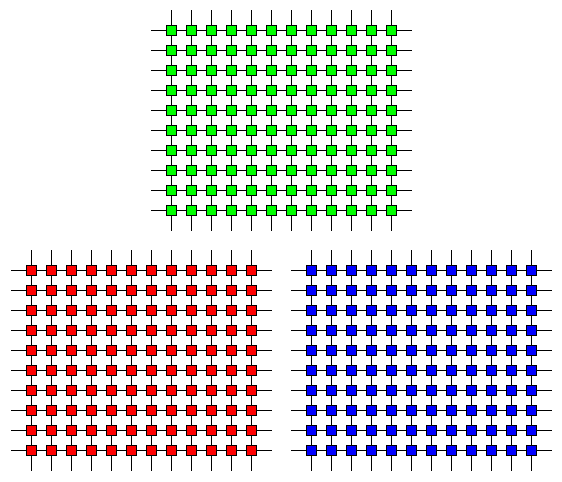 |
| Obr. 3 – Vzorky barevných kanálů po interpolaci |
K dopočítání chybějících vzorků je možné použít různých metod. Nejjednodušší způsob je vždy s každou buňkou uvažovat její tři sousedy ve čtveřici – např. vlevo, nahoře a šikmo vlevo nahoře. Chybějící hodnoty se v daném bodě doplní vždy hodnotami sousedních buněk patřičné barvy. Tento způsob ovšem není nic jiného, než obyčejná interpolace nejbližším sousedem provedená u každého z kanálů. Podobně jako v případě zvětšování a zmenšování obrázků i zde interpolace nejbližším sousedem dává velmi slabé výsledky. V praxi se proto používají složitější metody interpolace, založené na modelech, které lépe vystihují realitu. Kromě obecných interpolačních metod zmíněných v seriálu o digitálních úpravách, jako třeba bilineární nebo bikubické interpolace, se zde používají i specializované metody vyvinuté speciálně pro tento typ dat. Velmi pěkný přehled hlavních metod zpracoval Ting Chen, jeden ze studentů Laboratoře informačních systémů Stanfordské univerzity, ve svém ročníkovém projektu A Study of Spatial Color Interpolation Algorithms for Single-Detector Digital Cameras. Zpráva obsahuje u většiny metod kromě popisu rovněž i jejich implementaci v Matlabu – dovolila jsem si tyto programy využít k vytvoření příkladů, které zde můžete vidět.
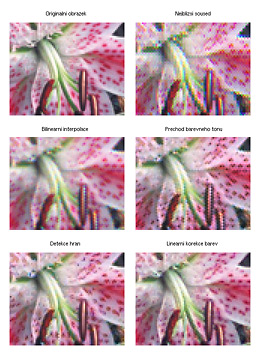
Na Obr. 4 jsou zachycené výsledky práce několika nejběžnějších metod na reálných datech. Abychom měli srovnání, jak by výsledek skutečně měl vypadat, vychází se z kompletního digitálního obrázku a výstup CFA sensoru se simuluje tak, že se u každého z kanálů ponechají vzorky pouze v bodech naznačených na Obr. 2. Zbylé 2/3 vzorků se zahodí a znovu doplní interpolací. Na výsledných obrázcích můžeme pozorovat typické artefakty, které vznikají při použití zejména těch nejjednodušších metod. Kromě zubatosti hran a ztráty ostrosti, se kterými jsme se setkali už při zvětšování obrázků, se zde objevují i posuny barev a zejména barevné zuby, vypadající jako “zipy” podél hran. Specializované metody, které provádějí interpolaci adaptivně, na základě analýzy dat v okolí každého bodu, jako např. na obrázku prezentovaná metoda založená na detekci hran nebo metoda lineární barevné korekce, dávají lepší výsledky. Jsou ale početně mnohem náročnější. Např. u tohoto konkrétního obrázku a této konkrétní implementace v Matlabu je interpolace nejbližším sousedem více než stokrát rychlejší než metoda lineární barevné korekce – zatímco interpolace nejbližším sousedem byla hotová za několik setin sekundy, při použití metody lineární korekce výpočet trval několik sekund. Jak je vidět, volba metody je kompromisem – za rychlost se platí kvalitou.
Barevní “duchové” a “zipy” podél hran jsou způsobené tím, že pro každý kanál známe hodnoty v jiných bodech. Je-li na obrázku někde strmý přechod (hrana), pak v interpolovaných datech má tendenci vzniknout přechod v každém kanálu v trochu jiných místech – výsledkem je pak barevné moiré kolem hran. Toto působí velmi rušivě zejména u monochromatických a téměř monochromatických námětů. Ukázka barevného moiré vzniklého na černobílém obrazci je na Obr. 5.
Metody, které pozici přechodů nějakým způsobem detekují a interpolaci výsledkům patřičně přizpůsobí, nejen do značné míry eliminují vznik těchto barevných artefaktů podél hran, ale výsledné obrázky jsou pak také opticky ostřejší. Někdy ovšem zvýšený lokální kontrast navozující dojem ostrosti může být až přehnaný – můžeme to pozorovat např. na tečkách na okvětních plátcích na zvětšených výřezech na Obr. 4, kde u interpolovaných obrázků v dolní řadě jsou tečky výrazněji definované a tmavší, než u originálu.
Jak je to s rozlišením obrázků z digitálu? Podívejme se nejprve na počty vzorků. Zanedbáme-li extra řady buněk na krajích, potřebné pro interpolaci, pak začneme-li s N vzorky z N buněk – N/4 červenými, N/4 modrými a N/2 zelenými, skončíme s N pixely, tj. N vzorky červenými, N modrými a N zelenými, čili celkem 3N vzorky (jak je vidět na Obr. 2 a 3, kde N=120).
Jak jemné detaily může obrázek z digitálního fotoaparátu obsahovat je dané hustotou původních vzorků. Nové vzorky vznikají na základě jakéhosi obecného modelu, který není schopný doplnit specifické detaily, které původní vzorky nedokázaly zachytit. Vzhledem k tomu, že hustota původních vzorků je nižší, výsledný obrázek nemůže reprodukovat detaily na té úrovni, na jaké to dokáže plnohodnotný neinterpolovaný obrázek o stejném počtu pixelů. Digitální fotoaparát
s CFA sensorem má tudíž fakticky nižší rozlišovací schopnost, než odpovídá uváděnému počtu pixelů.
Tvrzení, že obrázek z digitálního fotoaparátu poskytuje stejné rozlišení jako standardní neinterpolovaný obrázek o třetinovém počtu pixelů, neboli 1,73x menší v každém směru, není zcela přesné, jelikož jednotlivé kanály jsou vzorkovány různě hustě, tzn. jejich rozlišovací schopnost (vyjádřená nejvyšší zachytitelnou frekvencí – Nyquistovou frekvencí) se liší. U červeného a modrého kanálu je v každém směru dokonce pouze poloviční;
zelený kanál poskytuje o něco větší rozlišení.
Vzhledem k tomu, že vzdálenost mezi vzorky každého ze tří kanálů je větší než jeden pixel, detaily o velikosti zhruba jednoho pixelu CFA data nejsou schopná zachytit. Představte si např., že fotografujete černobílou šachovnici, která má čtverečky tak drobné, že na jeden čtvereček připadne přesně jedna buňka sensoru. Pokud by každá buňka měřila intenzitu všech tří kanálů, dostali bychom opravdu černobílou šachovnici. Nicméně zde, vzhledem k tomu, že buňky CFA sensoru jsou citlivé jen na jednu barvu a jsou rozmístěné jako na Obr. 1, tak výsledek bude takový, že všechny zelené buňky uvidí např. bílé čtverečky, zatímco všechny modré a červené buňky černé. Tj. (za ideálních podmínek, pomineme-li šum vznikající při snímání a pod.) všechny zelené vzorky budou mít hodnotu 255 (bílá má RGB složky 255, 255, 255) a červené a modré vzorky 0 (černá je 0, 0, 0). Úplně stejná data ovšem dostaneme, budeme-li fotografovat jednolitou jasně zelenou plochu (s RGB komponentami 0, 255, 0)!
Algoritmus dopočítávající chybějící hodnoty nemá absolutně žádné vodítko, které by naznačovalo, zda šlo o černobílou šachovnici nebo o zelenou plochu. Jsou to deterministické funkce a nemůžou dát pro stejná data pokaždé jiný výsledek. Navíc zde nemluvíme pouze o dvou různých obrázcích, pro která budou data stejná, ale o nekonečně mnoha takových obrázcích! Stejně dobře totiž mohlo jít o šachovnici černo-zelenou, černo-žlutou, zeleno-žlutou apod., v nekonečném množství různých odstínů (pomineme-li diskretizaci hodnot barev). Nebo ani nemuselo jít o šachovnici, ale o jeden z mnoha jiných vzorů např. o pruhy široké jeden pixel.
Takto jemná textura reprezentuje příliš vysokou frekvenci, přesahující Nyquistovu frekvenci pro danou hustotu vzorků. Data ji nedokáží zachytit. Žádný výpočet ji nemůže z dat, ve kterých není zachycená, zrekonstruovat. Kde nic není, ani smrt nebere. Toto je zachyceno na Obr. 6. Jak vidíme, ve všech případech je výsledkem interpolace takovýchto dat jednolitá zelená plocha. Vzhledem k tomu, že jednobarevné plochy se v obrázcích vyskytují velmi často, má to smysl. Metoda, která by pro takováto data (tzn. i pro jednobarevné zelené plochy) dávala šachovnici nebo pruhy, by v praxi nefungovala příliš dobře. Model o který by se opírala, by nebyl vhodný model pro reálné obrázky.
 |
 |
| Obr. 6 – Selhání u drobné textury. Zvětšeno 3x. | |
Výše uvedený příklad je sice poněkud akademický a v praxi k takhle extrémním situacím zpravidla nedochází, nicméně to, že data ze sensoru uspořádaného jako na Obr. 1 nedokáží detaily o velikosti zhruba jednoho pixelu zachytit, je patrné např. i na Obr. 4. Všimněte si, že žádná z metod interpolace nedokázala věrně zreprodukovat drobné tečky na okvětním plátku. Tenké čáry na Obr. 5 také působí problémy.
Takže abych to shrnula: Obrázky obdržené digitálními fotoaparáty s CFA sensorem jsou interpolované. Dochází k navýšení objemu dat na trojnásobek a tvrzení, že skutečná rozlišovací schopnost odpovídá třetinovému počtu pixelů, je sice velmi zjednodušené, ale má poměrně blízko k pravdě. Ondřej Neff se mýlí, když tvrdí, že se zde interpolace neprovádí – nebo, nověji, když interpolaci v tomto kontextu odmítá interpolací nazývat, viz dodatek k jeho článku Co je interpolace na DigiNeffu. Z matematického hlediska totiž zcela jasně jde o interpolaci a tento termín se též používá i v odborné literatuře týkající se problematiky CFA sensorů (viz např. obsáhlý seznam referencí v Ting Chenově zprávě). Zmatek sem nevnáší ti, kdo používají termín interpolace, ale Ondřej Neff. Mlhavý pojem “komparace” který propaguje, pouze mate a zastírá podstatu věci. Nepatří do slovníku odborníka, ale do kategorie klasických marketingových triků. Většina zákazníků má zafixováno, že interpolace = podvod, a pokud se podaří zamaskovat, že jde o interpolaci, a vzbudit dojem, že se jakousi zázračnou komparací z hodnot buněk vytvoří plnohodnotná data, je to nepochybně plus. Vysvětlení na stránkách Foveonu, které Ondřej Neff v dodatku ke svému článku Co je to interpolace označil za účelové zneužívání termínu interpolace, naopak vůbec žádným marketingovým trikem není. Toto vysvětlení je sice poněkud zjednodušené, leč v principu zcela pravdivé.
Představa Ondřeje Neffa, že k umělému navýšení objemu dat zde nedochází a obrázky produkované digitálem s CFA sensorem jsou neinterpolované, plnohodnotné, protože se barvy doplní na základě porovnání hodnot sousedních buněk, přičemž trik spočívá v tom, že každá buňka se použije víckrát, je naivní a zcela mylná. Zázraky se nedějí.
Je to přesně totéž jako u zvětšování obrázků. Tam se také RGB hodnoty každého starého pixelu účastní výpočtu vždy několikrát. Nicméně tím se ztracené detaily nenahradí. Nyquistova frekvence je Nyquistova frekvence. Cokoli menšího je nenávratně ztraceno.
Znamená to tedy, že výrobci digitálních fotoaparátů jsou podvodníci? Podle mě nikoli. Udávat faktické rozlišení a nikoli počet pixelů výsledného obrázku by bylo poněkud komplikované (ona to není tak docela ta třetina, která bývá často zmiňovaná), nepraktické a jen zbytečně matoucí. Interpolace u CFA sensorů funguje velice dobře a lepší cenově dostupné a v praxi použitelné technické řešení momentálně neexistuje. Normálnímu uživateli může být celkem jedno, jestli obrázky, které svým digitálním fotoaparátem získá, jsou interpolované nebo ne. Na druhou stranu, pokud se provádí exaktní srovnání rozlišovací schopnosti digitálních fotoaparátů a skenerů, či filmu, pak je potřeba skutečnost, že u digitálních fotoaparátů s CFA sensorem se data doplňují interpolací a faktické rozlišení obrazu je nižší, než by odpovídalo počtu pixelů, vzít v úvahu.
Závěrem bych ráda poděkovala Radku Tezaurovi, který mě na Ting Chenovu zprávu upozornil.




foveon 3x
tak aby to uz napriste bylo jasne, Foveon prisel s cipem, ktery ma skutecne vsechny 3 barvy v jednom sensoru 🙂
Tak muzem jen doufat, ze to bude skutecne uspokojive fungovat a postupne (rychle) to nahradi dnesni cipy.
Na PMA uz bude tento cip v digitalni zrcadlovce Sigma (3,3MB).
Je to tedy srovnatelne s 9MB dnesnim cipem ? 🙂
RE: foveon 3x
Jak jsem uvedla v clanku, tak tvrzeni, ze cip s “trojbarevnymi” bunkami je srovnatelny s cipem s “jednobarevnymi” bunkami o trojnasobnem rozliseni je jen velmi zjednodusenym srovnanim na zaklade hrubeho objemu dat pred interpolaci, ktere zcela ignoruje dulezitou skutecnost ze u CFA sensoru jsou jednotlive barvy vzorkovany v ruznych bodech a ruzne huste. Co se tyka X3 technologie Foveonu, je to nepochybne krok dopredu, ale s jasanim a mavatky bych pockala az jak se cip osvedci v praxi. Rozliseni neni vsechno. Zalezi na mnoha dalsich faktorech, napr. jak jsou vysledna data zasumena a jakeho budou schopni u takoveho chipu dosahnout dynamickeho rozsahu, barevne vernosti obrazu a pod. Dovedu si predstavit, ze usporadani ve vrstvach bude mit svoje specificke problemy. Nicmene da se cekat, ze vyvoj pujde v tomto smeru dopredu a casem budeme opravdu u digitalu odlisovat mene kvalitni, interpolovane, s CFA cipem, a neinterpolovane, s cipem s “trojbarevnymi” bunkami.
a co film?
Moc pěkný a přehledný článek. O. Neff má matoucích tvrzení na digineffu opravdu dost, viz např. posouzení počtu čar/mm u digitálů.
V souvislosti s rozlišovací schopností digitálů a skenovaných filmů by možná stálo za to i zamyslet se nad vlivem náhodného rozložení zrn či barviva při skenování – tedy myslím trochu odborněji se zamyslet.
RE: a co film?
To mi ovsem prijde spis jako namet na vedecky grant, nez na clanek pro Paladix. 🙂
Bravo
Vyborny clanek – diky za nej. To, ze jsou obrazky z digitalu interpolovane, to vim, ale takhle nazorne predvedene jsem to jeste nikde nevidel. Dobra prace 🙂
Co se Digineffu tyce — uz tam hodne dlouho nechodim. Muj pocit z nej je, ze p. Neff si na odbornika na digitalni fotografii spis hraje, nez ze by jim opravdu byl.
RE: Bravo
Naprostej souhlas, fakt super článek. Jen tak dál a houšť.
Uvaha
Pri skumani argumentov autorov oboch spornych nazorov som narazil na nasledovny problem: pri snimani sachovnice, kde jedno policko = jedna bunka CCD (alebo inak povedane, pri vzorkovani frekvenciou rovnou dvojnasobku vstupnej frekvencie) skutocne dostaneme vysledky, ake popisuje radka vo svojom clanku. Ked vsak sachovnica, ktoru snimame, bude dvojnasobnej velkosti, t.j. jedno policko pripadne na stvorec 2×2 bunky CCD (t.j. zdvojnasobime periodu vstupu), dostaneme na vystupe skoro spravny vysledok – pixely v strede stvorcov 2×2 na sachovnici budu biele, resp. cierne, a ostatne – hranicne pixely nadobudnu jednu z farieb C, M, Y, G. Kazdopadne sme vsak navzorkovali povodnu frevenciu, perioda vystupu je skutocne 4 pixely. Matematickymi metodami popisanymi v clanku sa da dosiahnut eliminacia zmienenych C, M, Y, G, co v konecnom dosledku znamena vernejsi obraz.
A teraz myslienkovy experiment: predlohu, t.j. sachovnicu s polickami velkosti 2×2 bunky CCD zacneme zmensovat a sledujeme, ako sa zachova vystup. Na vystupe bude zrejme vznikat rezonancia, ktora sa v obraze prejavi ako moire, ale stale sme navzorkovali povodnu frekvenciu, i ked nepresne. Tu prichadzaju k slovu znovu matematicke metody, ktore umoznuju moire eliminovat – t.j. presnejsie rekonstruovat vstup. Sachovnicu dalej zmensujeme a moire vnimame az do okamihu, ked velkost jedneho policka sachovnice bude rovna velkosti jednej bunky CCD. Vtedy sa moire prestane prejavovat a na vystupe bude homogenny obraz, z ktoreho uz nedopocitame nic.
Zaver: na zaklade uvedeneho sa mi zda, ze pre vzorkovaciu frekvenciu vacsiu (ale nie rovnu) nez dvojnasobok frekvencie vstupu vieme na vystupe zrekonstruovat povodnu frekvenciu. Cim je perioda vstupu vacsia, tym kvalitnejsie vieme reprodukovat vystup. To ale znamena, ze rozlisovacia schopnost digitalnych pristrojov sa skutocne blizi poctu pixelov, ale velmi zalezi na pouzitej metode interpolacie. Je tento moj zaver spravny?
B. Stepanek
RE: Uvaha
Zasadni chyba v teto uvaze spociva v predpokladu, ze jsme “navzorkovali puvodni frekvenci, jen nepresne, a ze vznikne moire, ktere matematicke metody budou schopne eliminovat”. Co se totiz stane je, ze jakmile je frekvence, kterou vzorkujeme (sachovnice je jen hrube priblizeni toho, co to frekvence je – je zde potreba brat trigonometricke funkce) vetsi nez kriticka Nyquistova frekvence, tak se tato prilis vysoka frekvence kompletne ztrati. Dostaneme data, ktera jsou zcela identicka s daty, ktera bychom obdrzeli pri vzorkovani jine, nizsi frekvence. Tomuto jevu se rika aliasing. Dobre je to videt na Obr. 10 v clanku o zvetsovani a zmensovani obrazku. Tzn. efekt je prakticky stejny, jako u prikladu se zelenou plochou, jen tu nevznikne rovna plocha, ale zvlnena – falesna frekvence nizsi nez ta puvodni. Zadna interpolacni metoda nemuze vedet, zda tato zcela identicka data patrila puvodne opravdu falesne nizsi frekvenci, nebo nejake vyssi (a existuje zde opet nekonecne mnoho takovych, ktere prichazeji v uvahu). Vzhledem k tomu, ze v obrazcich zpravidla prevazuji nizsi frekvence, budou mit interpolacni algoritmy vhodne pro obrazky tendenci vyprodukovat spis onu falesnou nizkou frekvenci. Pro polovicni pocet vzorku je Nyquistova frekvence polovicni, tzn. budeme-li fotografovat napr. neco, co je modre, pak maximalni rozlisovaci schopnost digitalu s CFA sensorem bude jak ve vodorovnem, tak i ve svislem smeru polovicni, nez naznacuje pocet pixelu na vystupu, a to bez ohledu na pouzitou metodu interpolace.
Clanek
Ondrej Neff nikdy netvrdil, ze se nemuze mylit. Snazi se podavat informace tak jak jim rozumi a jake jsou v dane chvili k dispozici a urcite to nedela proto, aby nekoho naschval uvedl v omyl. V tomhle je clanek zbytecne utocnej. Jestlize se autorka v clanku priblizila ke skutecnosti vice nez pan Neff, tak verim, ze si to pan Neff overi a sve stranky opravi. Informacim uverejnenym v clanku naprosta vetsina uzivatelu digitalu nikdy neporozumi a ani je nemohou ovlivnit, proto maji pro ne tyto dohady cenu dohadu, ktere se tahly celym stredovekem. Byly to dohady o hmotne ci nehmotne podstate andelu.
RE: Clanek
Bohuzel nemate pravdu. S Ondrejem Neffem jsem (a nejen ja) vedla na toto tema dlouhou diskusi jak na fotopruvodci, tak i soukrome, po e-mailu. Pan Neff veskere logicke argumenty odmita a s overovanim si take prilis mnoho prace nedal, a to i pres to, ze lide, kteri mu psali, jsou profesionalove v oblasti matematiky a zpracovani digitalniho obrazu, a je tudiz dost pravdepodobne, ze vedi o cem mluvi a na tom, co rikaji, asi neco bude. Jedina oprava, kterou provedl, je prave onen dodatek k jeho starsimu clanku o interpolaci, ktery je v mem clanku zmineny. To byla jedna z hlavnich pricin, proc jsem tento clanek napsala. Musim rict, ze tento jeho pristup je pro mne osobne hodne velkym zklamanim. Ondreje Neffa mnoho lidi povazuje za nejuznavanejsiho ceskeho odbornika v oboru digitalni fotografie a jeho nazory berou za bernou minci. Myslim, ze pokud napise neco, co evidentne neni pravda, zaslouzi si to uvedeni na pravou miru a pokud to neudela sam, je potreba, aby to udelali jini…
Co se tyka toho, ze vetsinu majitelu digitalu mnohe podrobnosti uvedene v clanku nezajimaji a neni potreba, aby jim rozumeli, plne s vami souhlasim – i kdyz zda se, ze s novymi chipy, jako napr. ten od Foveonu, problem interpolovany vs. neinterpolovany obraz zacne v budoucnu mnohe zajimat a uz to nebude jen o te hmotne podstate andelu. Je ovsem mezi nami i mnoho takovych, ktere takovehle veci zajimaji uz dnes, a prave tem je muj clanek urceny.
RE: RE: Clanek
Vubec se mi nelibi vase utocne poznamky.
Nejsou vhodne, mistne, nesvedci o Vasem dobrem vychovani, vkusu, taktu a socialni inteligenci.
Nevzpominam si, ze by pan Neff, nebo jiny slusne vychovany gentleman psal neco o jakesi -censored-, ktera obcasne prispiva na paladix, jejiz clanky nejsou nijak svetoborne, jejich stylistika nic moc a jejich obsahovost, nebo ucel nejasny! Nevim pro koho jsou vase clanky urcene. A priste se, prosím, vystrihejte osobnich invektiv vuci panu Neffovi. Je dobre si uvedomit, ze pan Neff je popularizator digitalni fotografie v tomto duchu je i koncipovan server digineff. Kdyby se vase clanky publikovali na digineffu, byl by to vysmech. Je to pro nejsirsi verejnost a je treba, aby byly podane v co nejsrozumitelnejsi forme, rozhodne ne v podobe kapitol VŠ skritp. P. Neff není vědec a digineff není výzkumný vědecký server. Snažte se to pochopit, není to těžké, z diskusí k vašim článkům vyznívá, že nejeden váš čtenář to již pochopil. Teď k vašim článkům. Jejich adresnost je nejasná. Pro nejširší veřejnost rozhodně nejsou. Pro profesionály a vědce také ne-ti to musí vědět. Pro studenty technik a jiných exaktních věd (můj případ) také ne, ti to rovněž musí znát. Jediná úzce profilovaná skupina, pro kterou to má nějaký faktický přínos jsou zvídaví amátéři digitálni fotografie, kteří si rádi rozšíří obzory a podohlédnou rádi, jak věci fungují. To je velmi malá skupina lidí a v relaci s tímto by měly být uměrné i vaše publikační ambice. Osobně jsem si vaše články přečetl, děkuji za ně, srozumitelné, trošku jsem si rozšířil obzory -co se týká color managmentu.
Ale nelíbily se mi -jako mnoho jiným čtenářů- vaše útoky vůči panu Neffovi. Jeho články mají ohromný přínos, nejsou vědecké- ale vězte že pro majoritu čtenářů jsou více přínosné články nevědecké avšak psané pěkným stylem zkušeného spisovatele!- než suchopádné, avšak sémanticky a faktograficky přesné vaše články. Připomínajicí opsané kapitoly učebních skript. Články, které dokáže napsat každý student doktorandského studia (MFF UK, nebo ČVUT) a každý kdo stojí v akademické chierarchii výše. Dokonce řekl bych že i mnohý student nejen doktorandského studia, ale jen vyššího ročníku VŠ.
Tomas.
RE: RE: RE: Clanek
Jsem rád, že zde máme dalšího “slušně vychovaného gentlemana”, který se pěkně podepíše a udá svoji e-mail adresu, aby s ním mohl člověk polemizovat mimo tento prostor, který je výhradně určen komentářům k danému článku – a ne k obecnému a nekonkrétnímu napadání někoho jiného.
Takže milý Tomáši, souhlasím s Vámi v tom, že pan Neff je popularizátor digitální fotografie. O tom není sporu. Jeho server k tomu také velmi významnou měrou přispívá. A je to i jeho zásluha (a nejen z webu, ale i z přednášek, které pořádá), že je digitální fotografie v ČR tak populární, jak je. Tyto zásluhy mu nikdo neubírá. Ale ani to není omluvou pro šíření zcela zjevných polopravd či nepravd, na což měl tento článek poukázat. A je úplně jedno, kdo to je. Kdyby to nebyl pan Neff, byl by to kdokoliv jiný, nemusíme se nikomu zpovídat a můžeme svobodně polemizovat s jakýmkoliv názorem, ať je jeho autorem třeba i pan prezident. A je svobodnou vůlí každého také polemizovat s našimi názory, v tom nikomu nebráníme. Pokud někde píšeme nesmysly nebo polopravdy, nechť nás na to kdokoliv upozorní.
A komu jsou adresované Radčiny články? Jistě ne Vám, protože Vy jste natolik vzdělaný, zkušený a slušný člověk, že už Vám nemohou přinést nic nového. Je škoda, že ty svoje bohaté zkušenosti také nedáváte na odiv široké čtenářské veřejnosti. Jak jste si jistě všiml, píše Radka články jak pro úplné začátečníky, tak i pro velmi pokročilé čtenáře. Každý si ale vždy svoje čtenáře našel, o čemž svědčí i to, že z prvních 50 nejčtenějších článků (z celkového počtu 719 článků – stav k 14.8.2003) napsala Radka 19 z nich (tj. má 38% podíl) a celkem bylo těch 19 článků k dnešnímu dni přečteno více než 105tisíckrát. To dává průměr více než 5500 přečtení na jeden článek. Jistě, věřím tomu, že Vaše články by měly minimálně dvojnásobnou čtenost, ale bohužel to není možné nikde ověřit – nebo pokud ano, dejte mi link, kde se na ně můžeme se zájmem podívat. Celkově je tedy jasně vidět, že Radčiny články jsou tak úzce profilované, je je rozhodně nikdo nečte, protože laika to jasně nezajímá a profík to samosebou ví. A proto ji mezi sebou rádi máme, protože my všichni, co tento server děláme jsme přesně tou cílovou skupinou – nejsme ani úplní laici, ale ani ne 100% profíci, abychom se něco nového nemohli dozvědět.
Na závěr Vám mohu doporučit jediné. Pokud Vás Radčiny články opravdu tak iritují, tak je prostě nečtěte. Určitě budete bez zbytečného rozčilování žít déle.
trochu vam narostly ramena!
Pokud povazuje nekdo pana Neffa za odbornika digitalni fotografie – jeho problem. Ani jsem nikde neslysel, ze by to pan Neff o sobe prohlasil.
Pro me je Digineff naprosto skvely pro zacatecniky, neni tam nic tezce nesrozumitelneho, zadne hrani si na vedu.
Proto mi nektere prispevky pripadaji jen jako vyroky tech, kteri uz zapomeli, ze taky nekdy zacinali a ted tezce prehlizeji \”ty pod nima\”.
Paladix je proste vice odborneji zameren, ale neprislusi mu hledet na ty mene znale z vysky. Proste pan Neff nema pravdu, tecka, konec, bez utocnych poznamek.
RE: trochu vam narostly ramena!
Nechci vubec na nikoho nahlizet zvrchu. Akorat me bavi si hrat na vedu (a proto se tim m.j. i zivim) a mam radost, kdyz si se mnou na vedu hraji i jini. O vede si myslim, ze je dulezita a jednou z mych profesionalnich deformaci je, ze kdyz slysim “no a co ze je to blbe, stejne je to jedno, prakticky vyznam to nema a nikoho to nezajima”, tak mi zacne jit pena od huby. Jsem jen clovek a snad mi to odpustite.
Co se Ondreje Neffa tyka, tak me svym pristupem opravdu velmi zklamal. Ano, DigiNeff je urceny hlavne zacatecnikum, ale myslim, ze i zacatecnici si zaslouzi, aby informace jim urcene byly -pokud mozno- pravdive. Ono to neni vubec snadne, zjednodusit veci tak, aby je lide pochopili a nepotrebovali na to univerzitu. Nejaka ta licence je potreba. Nicmene veci, ktere jsou v principu chybne, by se tam prece jen vyskytovat nemely. Zacatecnik nevi, veri vsemu a pak se pokousi dal stavet na necem (nebo i siri dal neco), co neni pravda. Pokrocily, ktery chyby najde, zase takovy zdroj prestane povazovat za seriozni a prijde tak treba o mnoho uzitecnych informaci, ktere pravdive jsou. Nevycitam Ondrej Neffovi, ze neco nevi nebo ze se dopustil chyby. To je prece zcela normalni. Chybovat je lidske, nikdo nevime vsechno a stale se ucime. Co me mrzi je, ze i kdyz ho hned nekolik lidi z oboru upozornilo, ze se dopoustil chyby, nesel veci na kloub a odbyl to velmi povrchnim zpusobem. To si myslim ctenari DigiNeffu nezaslouzi a neslucuje se to ani s novinarskou etikou.
RE: trochu vam narostly ramena!
Chtel bych vyajdrit svuj nazor a to predevsim k clankum Jana Novaka a Jirky.
Zaprve jsem si nevsiml, ze by se nekdo nad nekym povysoval a “prehlizl ty pod nema”. Co se tyce stranek Digineff, beru je za dobry prehled digitalnich fotografii. Nechapu ovsem proc branite samotneho pana Neffa. Pokud se nekdo myli, je to zcela bezne, ba co vic, na zaklade omylu se ucime! Proto, povazuji za tento clanek za povine upozorneni, ci upresneni na clanek, ktery byl na digineffu zverejnen. Sice o nic nejde, jedna se preci o nejaky clanek na webu. Tak by se to dalo brat, pokud by jsme sedeli nekde v hospode a povidali si o digitalnich fotkach. Ovsem Neff je, da-li se to tak rici, vlastnikem digineffu a odpovida za clanky, ktere inzeruje do sveta a je za ne odpovedny.
I ve vede, a predevsim v ni, by mela existovat moralka. Pokdu nejakemu problemu nerozumim do te miry, abych o nem psal clanek, radeji reknu “sorry, to nezvladnu” nebo tvrdim jen to, co mam overene a co mi je jasne. Pokud tak nekdo necini, je to nemoralni. Pan Neff je profesional a je to jeho prace, proto by se podle me, mel zachovat jinak a zmineny clanek alespon upravit.
Nechci zde kazat o moralce, ale tvrdit, ze je lepsi “spatny clanek, kterymu rozumim” a ne “spravny a podrobny clanek, kteryt nechapu” je podle meho nazoru zcestne. Nejsem zadny vedec, ale myslim ze obcas popremyslet a snazit se proniknout do problemu je prospesnejsi, nez psat ze je to k nicemu.
Pochopit zaklady by mel byt prvni krok…
Jsem rad, ze se na Paladixu objevuji clanky – a myslim specialne Radciny – ktere se venuji i teorii. Myslim, ze clovek by mel vedet s cim pracuje a jake jsou jeho moznosti a limity. Stejne jako ridic, ktery nic o autech nevi, neni nejlepsim ridicem, fotograf bez znalosti principu jeho pristroje, neni v pravem smyslu fotografem, ale clovekem, ktery si obcas udela par obrazku pro radost. Na tom neni nic spatneho, ale nesouhlasim s tim, ze napln tohoto clanku postrada smysl a je jen “dohadem”. Pro me osobne smysl ma a jsem rad, ze jsou lide, jako Radka, kteri vedi o cem pisi a umeji to ctenari perfektne podat. Mym zboznym pranim je, aby takove clanky vychazely na Paladixu dal.
format obrazku
Mel bych malou poznamku. Prijde mi nestastny u takovehoto tematu vystavovat ukazkove obrazky ve formatu jpg se ztratovou kompresi (http://www.paladix.cz/rs/img.php?ido=11716). Chapu ze 1,1 MB ku 196,1 KB je podstatny rozdil, ale navrhoval bych alspon odkaz na originalni obrazek.
Nekdo jiste muze namitnou, ze je stejne zkomprimovany i originalni obrazek. Ale je take mozne, ze komprimator chybu metody vystihne a obrazek jeste vice zmrsi, nez je tomu ve zkutecnosti a neni proto mozne metody objektivne porovnat.
RE: format obrazku
Kdyby se jednalo o papirovy casopis nebo knihu, patrne byste vydavateli veril, ze tistena podoba obrazku, kterou pred sebou vidite, dostatecne verne reprezentuje original. Zkuste mi tedy take duverovat a predpokladat, ze jpegy a gify vytvarim velmi peclive v takove kvalite, aby ukazky nebyly znehodnocene viditelnymi artefakty od ztratove komprese nebo konverze do 256 barev, a ze co vidite na nich, bylo skutecne patrne i na originalu, nez jsem ho ulozila ve formatu vhodnem pro web. Pokud se chcete presvedcit, original ukazky detailu kvetu interpolovaneho ruznymi metodami ulozeny bezztratove v tiffu je k dispozici zde.
Digital vs. Zenit E
tak ma napadlo, ze ak ma “sunka” objektiv Helios 2/58 rozlisenie 80 ciar/mm, tak potom:
Pri velkosti policka 36x24mm to bude: 2880×1920=5529600
…a kedze je to na film a nic sa tam neiterpoluje, vychadza rozlisenie 5529600×3= cca. 16Mpixelovy digitalis (!?)
-opravte ma niekto ak je to blbost-
RE: Digital vs. Zenit E
No, musim ta sklamat, Helios ma pri clone 8 a v strede obrazku 60 ciar/mm a na okraji 50. A pri clone 2 je na okraji 35. Ale to vobec nevadi, zakladna myslienka je spravna, iba cislo nesedi. Tak som to trochu preratal:
Budem ratat s hodnotou na okraju, lebo ta je zarucena a stred moze byt aj trochu nespravne zaostreny. Okrčem toho tym znizim vyslednu hodnotu co bude spravne, lebo fotka o rozmere 10×15 nezodpoveda uplne policku o rozmere 36×24 (fotka ja vzdy vyrez – aj ked iba malicky).
Clona 2 (35 ciar/mm): 3,27 megapixelu (24*35+36*35*3)
Clona 8 (50 ciar/mm): 6,48 megapixelu (24*50+36*50*3)
este idealny pripad pri clone 11
Clona 11 (stred – 60 ciar/mm) : 9,33 megapixelu (24*60+36*60*3)
Tolko teoria. Prax vyzera ale inak a co som videl fotky z digitalisov a porovnaval ich s mojimi fotkami zo Zenitu EM (rok vyroby 1975) s objektivom Helios 44-2M, tak mozem kazdeho uistit, ze fotky so Zenitu boli omnoho lepsie, namali “vyblite” farby (cervena bola cervena a nie ruzova – film Fuji Superia 100 alebo Agfa Vista 100 !!!Pozor, neskusat s filmami Kodak GOLD, lebo aj tam mozu vzniknut vseliake farby – Kodak vrele neodporucam), mali lepsiu ostrost a krajsiu kresbu detailov. Okrem toho nemali “rybie oko”, ktore vzniklo pri snimani digitalisom so “smejdovou – kompaktnou optikou.
Zhrnutie:
Digitalis je SROT!!! a nema ani na Zenit E s objektivom Helios z roku 1968! (aj Industar staci…) Navyse je digitalis drahy a nikdy by som ho za tu cenu nekupil!
Vsetci co rozmyslate nad kupou digitalisu sa zamyslite a kupte si za tie peniaze radsej nejaku kvalitnu zrkadlovku. Alebo si kupte za smiesne peniaze Zenit E (odporucam skor Prakticu rady L) a ostane vam dost panazi na celuloidove filmy (ale urcite nekupujte Kodak Gold a filmy typu Ctyrlistek Color) a na ich spracovanie.
RE: RE: Digital vs. Zenit E
Digital a film takhle jednoduse srovnavat nejde, jednoduche prepocty tohoto typu nefunguji. Obraz porizeny digitalem a obraz na filmu maji zcela
rozlisne charakteristiky, ktere delaji prime srovnani obtiznym (obraz na filmu je tvoreny nepravidelnym zrnem,…). Navic, vzhledem k tomu, ze mezi jednotlivymi modely digitalu jsou co do kvality obrovske rozdily, tak jakekoli srovnani digitalu a klasiky bez uvedeni, o ktere konkretni modely se jednalo, nema vubec zadnou vypovidaci hodnotu. Hodit vsechny digitaly do jednoho pytle a prohlasit je za srot je holy nesmysl. Digitaly vyssi tridy si dnes kvalitou obrazu s kinofilmem uz nezadaji. Nemluve o tom, ze kvalita obrazu neni jedine srovnavaci meritko.
RE: RE: RE: Digital vs. Zenit E
radka, samozrejme, moj prispevok nie je na 100 percenet pravda, pravde by sa to blizilo iba pri idealmon filme – minimalne zrno, etc…. Nehadam sa, ale chcel by som odpovedat: Porovnaval som fotky so Zenitu EM (800 Sk) a Olympusu C2 za cca. 15 000 Sk (cize okolo 10 000 Kc). Cize toto bola fakt ta najnizsia trieda digitalisu. Ale porovnaval som to aj s digitalom za 35 000 Sk (znacku neviem) a stale som nemal pocit, ze je to kvalitne (neprirodzene farby a navyse ten fotak bol strasne neprakticky – ked chcem exponovat, tak po stlaceni spuste si najprv zaosti a nastavi expopziciu (to je este v poriadku, tak to ma byt), pri dalsom stlaceni exponuje, ale (a v tom je problem) trva mu to pol sekundy, kym naozaj odfoti scenu. Cize na sportovu fotku absolutne o nicom. Fotil som s tym futbalovy zapas, takze viem o com to je a tiekli mi z toho nervy. Navyse ten zabudovany Zoom objektiv nebol nic moc (ked este k tomu zacal digitalne zoomovat, tak to ma fakt nastvalo, lebo kvalita = horsie ako Kodak PJ800 po expiracii, takze digital zoom som ihned vypol), to by som si radsej hodil na Zenit telac o ohniskovej vzdialenosti 200 mm a 200 ASA (alebo 400) film a je pohoda. Mal som ale moznost hrat sa aj digitalom za 100 000 Sk. To bolo dost ine, klasicka zrkadlovka ako sa patri (znacku som zabudol). Tak taky digital by som bral aj ja. Ale co vsetci vypravaju o digitaloch, tak vravia, ze si kupia nejaky do 20 000 (hladaju akcie) a je velmi tazke ich presvedcit o tom, ze to nema zmysel a ze to foti na prd. Vzdy im vravim: Kupte si radsej dajaku zrkadlovku ako ten digital. Alebo, ked chcete, tak potom digital za 80 000 Sk a vyssie. Totiz o tych si myslim ze kvalitou sa uz priblizuju ku klasickemu filmnu. Ale ta cena… Ked si to niekto kupi, tak sa strachuje, ze mu to na dovolenke pri mori niekto slohne, stale je v strese a ani si poriadne neoddychne. Keby som isiel na dovolenku, tak naschval by som zobral iba Zenit EM (Prakticku B100 + objektivy by som nechal doma) a mal by som pokoj a klud, lebo aj keby to niekto slohol (co by sa mu vobec neoplatilo), tak by ma to az tak netrapilo. Ale dopocul som sa o jednej novinke, co sa udajne vyvyja – nejake digitalne snimace, ktore sa daju vlozit do klasickej kinofilmovej zrkadlovky miesto plechu, ktori pritlaca film a elektronika k tomu je v mieste filmovej kazetky. To by ma moc zaujimalo, co to je, kolko to stoji a aku kvalitu to ponuka. Keby ste nahodou vedeli co myslim a keby to existovalo, tak napiste. Dakujem. (ta predstava – Zenit EM digital…. :-))
RE: RE: RE: RE: Digital vs. Zenit E
Nezlobte se, ale to co jste napsal je strasna legrace. Cele me to pripada jako kdyby jste mel akcie vyrobcu filmu nebo nevim ceho 🙂 To je jeste legracnejsi nez kdyz ctu v Stereo-video, ze CD maji studeny zvuk a proto zasadne kupovat gramo a vse ostatni vyjma studenosti/teplosti zvuku je pomijeno. Kazdy je v nejakem oboru expert a nekteri to proste neunesou. Zcela jiste rozumite fotografovani vice nez ja, ale aplikace vasich znalosti je zcela mimo. A vite co je nejdulezitejsi ve vasi uvaze? To, zdali ten clovek, co sezene v akci vytouzeny digital pod 20 000 Kc, napriklad Olympus 2100UZ za 499 EUR je SPOKOJEN. To je jedine hledisko. Popravde receno, mam nereprezentativni vzorek cca 10ti lidi z meho okruhu znamych, kteri presli na DIGI, nespokojen byl jeden – koupil si nejaky HP za cca 28 000 Kc a byl nespokojen s snimky ve spatnych svetelnych podminkach. Nadaval, fotoaparat prodal a hledal nejakou analogovou zrcadlovku, protoze tu co mel pred tim HP prodal. Nakonec koupil Nikon Coolpix 5000 a byl blahem bez sebe. Kdybych byl zcela mimo, mohl bych si z techto 10ti pripadu myslet ze analog jsou srot. To si ale nemyslim a opakuji, ze jedine meritko je jake ma dotycny fotograf pozadavky a zdali je s aparatem spokojen. Nic obecneho neplati a nikdy platit nebude. Nic ve zlem.
RE: RE: RE: RE: RE: Digital vs. Zenit E (tych “RE:” zacina byt az moc 🙂
Samozrejme, davam Vam za pravdu, ze vysledok zavisi od toho, ci je dotycny majitel fotaku spokojny. Spokojny s kvalitou snimku. Nuz, mne to je jedno – nech si pre seba foti co chce, kolko chce a ako chce. Ale ked mi to doense domov a vravi mi aby som do dal na internet, pricom ja mam so Zenitu ovela lepsiu fotku, tak je na MNA nastvany ze som to tam nedal. Potom sa vypytuje ze preco atd. Ked mu zacnem vysvetlovat ake to ma hnusne farby, rybie oko, ake je to rozmazane, vyblite a pod., tak je strasne urazeny. Ze on chce mat tiez fotku. Ja som mu povedal: Ked budes mat naozaj dobru, alebo exkluzivnu fotku, tak tam pojde. Samozrejme dost vela zavisi aj od toho, z coho clovek prechadza na digital. Ak ma dajaky kompaktny serbel, tak digital sa mu bude zdat urcite lepsi, lebo kompakty nerobia bohvie ake fotky (nech su tie kompakty akekolvek). Ale ked niekto vymeni zrkadlovku za digital, tak uz nemusi byt spokojny. Jedine ak si kupi digital za 50 000 Kc a vyssie. A mozem Vas uistit, ja ziadnu akciu od vyrobcov na filmy nemam, iba treba vediet KDE filmy kupovat a napr. FUJI Superia 100/36 sa da zohnat v pohode za 90.- Sk a AGFA Vista Eye Vision 100/36 za 77,50.- Sk. To su uz poloprofesionalne filmy s patricnou kvalitou. Este Vam vravim ze nie som profesionalny fotograf (to by som urcite nemal Zenit EM ani Prakticu B100), fotografiu pouzivam na dokumentacne ucely, ako hobby a preto, ze ma to bavi. To, co mozem robit s klasickym fotakom – napr. Zenit EM, s cb filmom – napr. FOMAPAN T200, vysoko prevysuje moznosti digitalu. Mna bavi robit experimenty s exponovanim, zvacsovanie v kupelni a pod (samozrejme fotim aj dost farebne). Fotenie neberem priserne vazne, ale od profesionala si vzdy necham poradit.
Okrem fotenia mam aj ine hobby (doprava, hram v kapele na bicie, zvukarcim a ine, rozumej PC). Nesustredujem svoju energiu iba na fotenie.
A ked uz pisete o platnach vs CD. Tak CD je vec pekna, teoreticky moze fungovat do nekonecna, na rozdiel od platne. CD je opticke medium (laser cita 1010100011101etc…), ma zvuk krystalovo cisty, jasny a vydrzi dlhsie ako platna (v praxi to nie je celkom tak, lebo aj CD sa moze poskrabat a pod.). LP ma kratsiu dlzku zaznamu, je mechanicke (ihla ide drazkou v povrchu platne, drazka ihlu vychyluje hore – dolu a zaroven dolava – doprava (stereo zvuk) a pri tom dochadza k vzajomnemu treniu a mechanickemu opotrebovaniu). Cize platna sa takto postupne “vyderie”. Nuz, tolko k mechanickej casti. CD ako medium zaznamenava zvuk vo frekvencii 44100 kHz, cize nad tuto frekvenciu zvuk uz nezachyti. Podobne je to aj pri velmi nizkych frekvenciach, CD jednoducho ma svoj obmedzeny rozsah. Klasicka LP platna je medium analogove, moze snimat frekvencie od nepocujem do nepocujem. Proste je dynamickejsia. Ale v konecnom dosledku vitazi CD, lebo pre ludske ucho je vysledny efekt tazko (alebo vobec) pocutelny a CD je kompaktnejsie a jednoduchsie na udrzbu. Ale jedna veta, ktoru som tusim pocul v akejsi rozpravke vravi: “Dobre, tak teda nie som vecna, ale za to ziva.” – To ako platna. Ale to uz zacinam pisat o inom ako o foteni, takze to sem naptri, lebo ma tu este niekto sprdne ze o com pisem. 🙂
RE: RE: RE: RE: RE: RE: Digital vs. Zenit E (tych \
Jakozto amater tak nejsa si jist, bych tedy vyjadril pochybnost, ze zvuk na CD ma 44 kHz. Rekl bych ze je to vzorkovaci frekvence a poslechova je 22 Khz. Jinak vidim, ze v tom mate jasno a vase nazory jsou konzistentni. Priklad s CD a deskou jsem tu dal jako absurdni priklad neceho co je mimo hru s jedinou vyhodou – sirsim poslechovym spektrem nebo jako bych to nazval (+moznost pro DJ po tom rejdit prstem) – sikovny pejsek bude mit zazitek na 25 kHz a to praskani a kolisani rychlosti a pakarna s vymenou desek mu nebude vadit – to udela panicek.
Jeste jsem nepochopil a prosim o vysvetleni te pasaze o tom, ze nedate kamaradovi na web fotografii ktera neni dobra. On ji chtel dat do nejake vasi fotogalerie? Nebo to hlidate komplexne? At je ji posle, ja mu ji uploaduji treba na foto.quick.cz – kdyz bude spatna a bude pod ni podepsany on, tak je to jeho ostuda. Ja mam dost sve ostudy s svymi fotografiemi 😉 Jelikoz je tento clanek z unora, predpokladam, ze tu nikoho neobtezujeme.
priklady tych fotiek
Dobre, mozem Vam ukazat konkretne priklady fotiek.
fotka c. 1
Zenit EM, fuji Superia 100, cas: 8 sekund, clona 8.
S digitalom by to nikdy takto neodfotil (nech ma presvedci o opaku a odfoti to tak).
Problem je v tom, ze ten digital nema taky dynamicky rozsah ako film a navyse ma strasne podanie farieb, co je vidno na dalsej fotke.
fotka c. 2
Fotka z Digitalu za 35 000 Sk. Bol som pri tom a to podanie farieb je uplne neprirodzene, najma cervena, ktora sa javi uz ako cerveno-oranzova, pricom to je klasicka cervena farba. Zelena farba transparentu je tiez nespravna, ani modra nesedi, am byt tmavsia. Pre porovnanie mate tu fotku spravenu zrkadlovkou EXA. Podanie farieb je verne.
—
Na stranke je uz dost nekvalitnych fotiek (aj mojich – starych), preto chceme pridavat uz iba fotky, ktore budu kvalitne, nebudu “vyblite”, dobre odfotene a pod. Aj ja tam mam fotky, ktore sa mi uz nepacia, ale uz sa pracuje na ich odstraneni a vyluceni z Galerie. Su to hlavne stare fotky, robene kompaktnym fotakom s cias ked som este nemal zrkadlovku. Niektore, ktore su zaujimave a vynimocne ostanu. Ale do buducna uz plati zasada – ak ta fotka nie je dobra, tak tam nepojde (jedine ze by bola niecim exkluzivna – nehoda a pod.).
Este by som dodal, ze vela zavisi od toho, ako mate nastaveny monitor, lebo zo skusenisti viem, ze na moze dost ovplyvnit vysledny efekt. Pracujem na EU na UVT (ustav vypoctovej techniky), takze mam moznost porovnavat ako fotka vyzera na viaceryach monitoroch. Na niektroych je ta ista fotka tmava, niekde dobra, inde zas svetla, niekde uplne vyblita. Takze aj o tom to je.
RE: priklady tych fotiek
Predeslu, ze jsem uplny laik ve smyslu abych mohl nekomu kritizovat fotky. Zcela subjektivne se me nelibi, ze na prvni fotografii padaji linie. A to hodne. Taky se me moc nelibi hloubka ostrosti. Pripada me, ze je tam sum jak krava, na druhou stranu je to foceno za svetelnych podminek, ktere by takto lowend digi nezvladl. Neodhadnu ani jak by to vyfotila napriklad Minolta DIMAGE 7 nebo moje oblibena Sony 707. Sorry, v noci takrka nefotim. Na druhe fotce z digi se me nelibi odlesk na strese tramvaje. Take me to pripada divne mazle v mistech kde se zachytavaji prejeti chodci. Treti fotografie pada tak, ze je to snad umelecky zamer 🙂 Je mi lito ale tezko soudit barvy, ono totiz zalezi na mnoho okolnostech, skoda, ze jste tu 10tku nefotil tim analogem v depu. Tezko neco porovnavat v depu za zarivkoveho osvetleni a venku. A priznam se, ze mam mnoho problemu s kvalitou, mam vypalena mista, padajici linie apod, ale barva je natolik subjektivni ze to ignoruji. Pokud je to zcela mimo pak prijdou na radu kurves. Pokud se nestane, ze ty barvy nechytne az Lab. KOukam na to 19 palcu SONY Trinitron.
RE: RE: priklady tych fotiek
Je jedno aky monitor mate. Ide o to, ako ho mate nastaveny, lebo aj ten najlepsi monitor moze podavat obraz zle (ovsem, tu je to VELMI subjektivne, kazdy si monitor nastavi ako chce, takze je velmi tazke vypravat o idealnom nastaveni, lebo to co sa paci Vam, sa nemusi mne a opacne).
Ja na prvej fotke nevidim ziadne linie, aj ked som si vytocil monitor. Co sa tyka sumu, ten sa mohol eliminovat pomocou levels, ktori som v tom case este tolko nepouzival a aj ked ano, mal som monitor nastaveny tmavise ako vacsina uzivaelov. Hlbka ostrosti sa moze zdat nizka, to je ale aj tym, ze som to dostatocne nevyostril, chcel som to mat take “makke”. Navyse co cakate od Heliosu? To je vzhladom k tomu cim to bolo fotene dost ostre. Spravil som si zvacseninu 18*24 (ci kolko to bolo, uz napamatam, venoavl som ju kamosovi k narodeninam) a je to ostre, verte mi. Okrem toho ta fotka dost dobre zachytava pocasie. Ked tak bolo, tak tak bolo. To mate tak, ako na tejto fotke. Proste je tam vidno ako to skutocne bolo, nie je to vobec umelo “vylepsovane”, zachytava to presne studene, vlhke, sychrave pocasie – to digital nespravi (teda taky do 35 000 Sk). Mozno sa Vam to pacit nebude, mne ale ano a zachytava to presne to co chcem. To iste mate aj na tejto fotke. Zobrazuje presne to, co ma. Ak sa Vam to nepaci, dobre. Nie je to super nasvietene, nema to vyrazne farby, ale o tom to je – tak to bolo. Priklad za dobreho pocasia mete tu. Tato fotka bola robena za jasnej noci a je to aj vidno. Napriek tomu je jasne vidiet rozne odtiene bielej farby na karoserii, fotka neposobi “tvrdo”. Mozno sa prave toto niekomui nepaci, mne sa to ale paci. Nerobi mi problem pomocou funkcie kontrast farby “vyblit”, ale to uz stracaju svoj “nadych” a atmosferu – to je to, co digital nezachyti. Podobny pripad mate tu. Fotka nie je idealna, priznavam, ale pochybujem ze z digitalu by som dostal rovnaky obraz (bavime sa o digitale do 35 000 Sk). Fotene Zenitom EM z ruky, objektiv Prakticar 200/4, cas 1/125, clona tusim 8, film citlivosti 100 ASA.
Tu je priklad umelo vyostrenej a vysvietenej fotky z digitalu. Tomuto sa chcem vyhybat – posobi to velmi umelo, vrchne vedenie sa na nebi straca. Fokta ja “vyblita” (tieto neziaduce efekty robia aj kompakty na kinofilm).
Este by som rad poznamenal, ze to co na iMHD je iba malicky zlomok z toho, co autori doniesli (vratane mna, ja nefotim vylucne MHD). Fotky z digitalov su iba tie najlepsie ake boli, keby ste videli tie ostatne, tak by sa vam mozno aj zaludok otocil. Tie farby, neostrost, kresba, etc. Hroza. Ja tiez niesom profesional, ale ked nieco fotim, tak to fotim nielen preto, lebo to tam zrovna je a cvak. Mne ide o to zachytit aj tu atmosferu, ktora tam bola. Ked sa na tuto fotku pozriem, ihned priam pocitim ten chlad a vlhkost. Este chcem upozronit, ze to je fotka z uplne prveho fimu, ktory som fotil v “ozajstnom” fotaku – Zenit EM. Objektiv som mal zaspineny, co je vidno na neostrosti laveho okraja obrazu, ale ked si to odmyslim, tak je to dobre. Ked pozeram fotky z digitalov, tento pocit ktori som napsal vyssie mi chyba. Nevyhodou digitalu je aj to, ze fotku vidim iba na monitore – to moze dost skreslit. Zle na takomto porovnavanii je aj samotne porovnavanie cez internet. Nizke rozlisenie fotiek na iMHD, ich kompresia JPG a pod. Vo velkej verzii to vyzera inak a tam sa tiez ukazuje rozdiel kinofim / digital. Okrem toho som rad, ze fotku mozem fyzicky drzat v ruke a pozerat si ju. To je daco ine ako sledovat monitor na stole. A vytlacit si digitalnu fotku – to by vyslo drahsie ako klasicky fotak na kinofilm.
Ked sme uz pri cene, tak si mozeme nieco preratat. Povedzme, ze film stoji 90 Sk (da sa zohnat aj za 77,50 – AGFA VISTA EYE VISION 100/36; ale povedzme ze 90, to je taka priemerna cena za 36 obr. film). Fotak + objektivy ratajme do 5 000 (Staci Prakticka rady L, aj ked ani Zenit nefoti vzhladom k tomu to to je a co to STOJI zle). Vyvolanie jednej fotky 10×15 aj s negativom je za 7 Sk. Na jeden 36 obrazkovy film bezne nafotim 39 snimkov. Takze mozeme ratat s touto hodnotou. 39*7=273 Sk. 273 Sk fotky + 80 Sk film = 353 Sk, zaokruhlime na 350. Teraz to porovnajme s digitalom za 35 000 Sk. Pri digitale mam jednorazovu investiciu 35 000 Sk + raz za cas nove baterky, flash karta, etc… Za tych 35 000 si kupim starsiu manualnu zrkadlovku (uplne staci 5000 Sk) + za 30 000 filmy a fotky. To zodpoveda 85 filmom, teda cca 3300 fotiek. Ja za mesiac vyfotim priemerne do dvoch filmov (podla okolnosti, niekedy viac, ked su akcie a niekedy menej, ked sa nic zaujimave nedeje). Takze rocne priblizne 24 filmov. (kedysi som fotil viac). 85/24 = 3,5 , zaokruhlime na 3 roky (mimoriadne fotenie povodni etc…). Teda ta investicia by sa mi vratila za 3 roky. To je dost dlha doba a navyse (A TOTO JE DOLEZITE!!!) ten digital za 35 000 Sk nesplna moje predstavy o foteni, ani moje naroky. Tie splnaju az digitaly v cenach odkolo 80 000 a vyssie. A navratnost 7 rokov si nemozem dovolit. Som obycajny clovek, som na civilke, dostavam 700 Sk mesacne. Aj ked budem zarabat, nebudem si moct kupit digital v tych cenach. To je dovod preco zostanem u klasiky.
RE: RE: RE: priklady tych fotiek
A co treba tyto fotografie?
S tou tramvaji jsem se pokusil neco udelat aby to nebylo tak vyblite
Jelikoz jste na tramvaje a ruzne pojezdy, tak vam sem hodim 2 fotky co fotil kamarad mym aparatem, digitalnim v ciste auto modu kdyz sel okolo: Loko, BUS a jednu co jsem fotil ja velice spatnych svetelnych podminek: hrad u vas
Jinak jste mi obstojne vysvetlil proc vy zustavate u analogu. Moc prenosne na dalsi jedince to ale asi nebude.
RE: RE: RE: RE: priklady tych fotiek
Tak jsem dnes dnes vzal do ruky puceny fotak a sel jsem na plaz fotit akci – volebal. Upozornuji, ze jsem nikdy v zivote nefotil nic co by se nejak rychleji hybalo, zejmena ne digitalne – fotim veskrze jenom hrady a makro. Fotak – (lowend-digi-C300) jsem nemel “v ruce”, proste jsem ho vzal a vyprasil kartu na kurt. Kdybych to umel a byl na ten fotak zvyknuty jiste by to bylo lepsi. Davam to sem proto, ze si myslim, ze se digi daji fotit dynamicke fotky. http://foto.quick.cz/krupinsky/beach/
Digital / vs Kinofilmova zrkadlovka
Dakujem za ukazky fotiek. Asi najviac sa mi pacila tato fotka. Ale aj ostatne boli dobre. Taky digital (Olympus E-20 P) by som ihned bral, ale to by som sa nikdy nedoplatil. FAKT!
Myslel som ze sa bavime o digitaloch v cenach okolo 35 000 Sk a nie o profesionalnych zrkadlovkach. Pri kompaktnych digitaloch svoj nazor zatial nezmenim – su to sroty pri porovnani so zrkadlovkami na kinofilm.
Nehnevajte sa, Vas pokus o znizenie “vyblitosti” fotky tramvaje je zbytocny, lebo ked ta fotka raz tie odtiene nema, umelo ich tam nespravime. Stale to neposobi prirodzene.
Fotka “SERGEJA” je vcelku foba, tu by som aj dal na net (po vystrihnuti). Problem je ten, ze na net davam zatial iba fotky MHD. Lebo svoje ine fotky (vlaky, mesto, priroda a pod.)nemam kam dat a som moc lenivy na to, aby som si vytvoril vlastnu stranku kde by som ich vystavil. Niesu hyperexkluzivne tutti-frutti, ale vidiet by sa rozhodne dali. Ale nevadi, to mas nezerie.
Na druhej fotke tolejbusu Škoda 7 Tr je uz vidno slaby dynamicky rozsah digitalu. Vrchne vedenie (troleje) sa straca, splyva s nebom. Nater je dost tmavy, ale to tak asi ma byt. Velika skoda oboch fotiek je, ze boli fotene moc z blizka, pri fotografovani sa mal vas priatel trochu viac oddialit od oboch vozidiel, lebo maju “rybie oko”. Ale to je iba detail.
K fotkam s palze: Dobre, ak Vam digitalny fotak exponoval v momente druheho stlacenia spuste, tak je to uplne v pohode. Mal som aj take v ruke, ale skoda ze som fotil ten futbal (alebo kopanu) prave s takym digitalom, ktory robil to co robil.
Chcel by som ragovat na tuto vetu: “Jinak jste mi obstojne vysvetlil proc vy zustavate u analogu. Moc prenosne na dalsi jedince to ale asi nebude.” Ani by som nepovedal. Ako neprofesional si nemozem dovolit digital za 100 000 Sk. A to iste plati aj o mojich kamosoch, ktori tiez fotia. Jeden ma Prakticu MTL 3, druhy Pentacon, ja som si konecne kupil Prakticu BX20 s objektivmi 1.8/50 mm a 2.8/135 mm za 3500 Sk, co bola fakt dobra kupa. Dalsi clovek ma akusi zrkadlovku Minoltu, etc… A nikto z nas neuvazuje s prechodom na digital. Dovody: 1. Cena, 2. kvalita dostupneho pristroja, 3. Zatial ziadne pozitivne ohlasy od ludi, ktori presli od zrkadlovky na digital (s kompaktou boli pozitivne ohlasy – to by som sa ale nedivil).
Este k financiam. Myslim si ze o takych 5 rokov, ked budu na trhu nove modely a vyvoj bude v tomto smere urcite rychlo napredovat, padnu ceny dnesnych digitalov. Potom mozno bude mozne zakupit najaky lepsi digital aj za prijatelnu cenu. To ze dnes este vylucujem prechod na digital nevznamena ze za 5 rokov tak nespravim. Vsetko je mozne. Nechajme sa prekvapit s cim novym pridu vyrobcovia, potom sa dnesne modely dostanu do lacnejsiej triedy.
oprava
V clanku som spravil chybu, zabudol som asi ” a spravilo to to co spravilo. Myslele som fotku toho Sergeja (rusen).
RE: oprava
No jsem rad, ze uz nejste alespon k digi tak prikry jako pred par dny. Vy do toho taky vnasite to, ze uz mate plne vybaveni, asi koupene nedavno a v takovem pripade se tezko nekam prechazi i kdyby bylo digi pozlacene. Navic jste civilkar a to pak je opravdu krize. Zrovna v patek jsem videl studenta jak z poslednich penez kupuje stareho Zenita za 800 Kc a uz mu zbylo jenom na nejaky 24/ film.
Naopak v nedeli vecer jsem byl v baru na svych dvou pivech a prisel tam zmokly fotograf, mel hlinikovy kufrik a vytahl SONKU 707 s 6 MPix cipem (SIC!!!) a ukazoval nejake fotky barmance. Tak jsem si prisedl a to jsem se dozvedel veci. Tu Sonku dostal od Sony pred rokem a ma ji jen tak na “cvakani”, protoze lidi nechteji platit a tak analogem foti jenom pro klienty kteri plati. (Mysleno 15 000 Kc/foto, nejakych 5000 Kc/foto ho nevytrhne – odhadem 🙂 V roce 1995 mel obrat 12 milionu, ted ma hubenych 1,5 milionu. Brecel mi tam, ze pro casopisy uz nema smysl fotit, ze to nezaplati. Proto skoro presel na digi, kde ma minimalni naklady a nebude hazet perly svinim. V atelieru foti zasadne na Sinar (F1?), stredoformat ma Mamyu, kinofilm je mrtvej – (to je vcelku moderni, nekdo rika, ze az za 5 let) 🙂 Koupil si i 12 Mpix stenu pro toho Sinara (celkove ma vybaveni asi za 6 000 000 Kc) ale nejak ho to nezaujalo (dela to 80 MB TIFy) a brecel ze uz nebude nic kupovat, ze se to nevyplati 🙂
fotenie a cena fotky
Iba by som chcel este napisat, ze sem-tam fotim aj pre noviny a za jednu fotku pytam 350 Sk. Mne to uplne staci. Takto som si zarobil na Prakticu B100. Fotil som jeden seminar so Zenitom EM (!!!) a uverejnili mi 9 fotiek. Pritom som tam vyfotil iba asi 20 obrazkov, takze ani naklady neboli extra velike. Bohuzial taketo akcie su zriedkave, ale potesia. 🙂 Ale nechcem tu tolko pisat, lebo Pavel Pola nam tu vynadal ze piseme o inych veciach ako k clanku. Vsak ked ho to nezaujima, tak nech to necita. Myslim si, ze sme (teda ja a W.K.) uz dosli k spolocnemu zaveru a zhodli sme sa. Vymenili sme si nazory, a o tom to tu ma byt. A so zaverom Pavla Polku suhlasim. O tom to presne je.
RE: RE: RE: priklady tych fotiek
vazeny pane, nechcem sa ostro vyjadrovat, ale zda
sa ze mate nejaky vazny komplex z toho ze niekto
si kupi fotak za x tisic a vy stale fotite s fotakom
ktoreho fakticka hodnota = 0 [resp. postupom casu sa stava zberatelskou kuriozitou]. Ja osobne tak isto vlastnim praktiku s ktoroum som vselico pofotil, nasledne jeden pentax a momentalne k svojej velkej spokojnosti fotim na 1.3MPx cannon a10. Ten fotak som si kupil ako obrazovy zaznamnik vo vypredaji a nasledne som bol velmi prijemne prekvapeny kvalitou ktoru produkuje, zrejme tym, ze ma asi slusnejsiu optiku ako viac mpx fotaky v tej cene za ktoru som to kupil :). Oproti beznym filmovym kompaktom su fotky ostrejsie a farebne ovela zivsie. argumentacia, ze na fotografovanie aby sa vasej praktike so zastaralym objektivom vyrovnal fotak, treba 80 tis posobi na mna mimoriadne komicky. Mozno neviete s digitalom pracovat z toho vyplyvaju vase problemy. Ps, co sa tyka toho “vybliteho podania farieb” dodal by som ze castejsie nez fotoaparat vinu nesie monitor na ktorom to pozerate ktory nema potrebny farebny rozsah. [momentalne mam v praci 3 monitory, na 21 trinitronovom hitachi su fotky fantasticky farebne podabne a ostre a na 20 starsom a bohuzial uz vypalenom tiez hitachi su fotky vyblite a dokonca aj neostre. [graf karty su matrox g450 a g400, takze v kartach to nieje]. [a predpokladam ze v skole asi monitorova spicka zrejme nebude].
RE: RE: RE: RE: priklady tych fotiek
este by som chcel dodat vyjadrenie k tomu casu,
neviem ako sa mozete divit ze reakcny cas digifotaku
ktory musi zanalyzovat scenu je dlhsi ako reakcny cas
praktiky. To je ako keby som tvrdil ze auta su naprd,
lebo kym ho clovek otvori, nastupi a nastartuje tak ten co siel pesi uz je na druhej strane ulice. ….
porovnavajte reakcny cas NAMACKNUTEHO digitaku [alebo takeho ktory umoznuje manualne ostrenie] vs praktika.
mne sa zda 0.1-0.3s zpozdenie celkom pouzitelne, hlavne ak fotak umoznuje fotit seriovo a da sa na to zvyknut a odfotit aj skutocne akcne sceny. [ten cas co ste uvadzali je zrejme (podla jeho trvania) cas ukladania fotky na kartu].
RE: RE: RE: RE: RE: RE: Digital vs. Zenit E (tych “RE:” zacina byt az moc 🙂
Musim nesouhlasit s nazorem, ze deska ma vyssi rozsah frekvenci. Vzhledem k mechanickemu zaznamu dat se tam (zvlaste u vysokych tonu a vyssich harmonickych slozek) musi projevovat setrvacnost (jehla, ac sebelehci, presne nekopiruje drazku, drazka mimochodem zase tezko muze presne kopirovat puvodni matrici). Vysledkem je zkresleni, ktere proste nekomu pripadne prijemnejsi nez zvuk CD.
Nechci ale tvrdit, ze CD zaznam je bez chyby. Vzhledem ke vzorkovaci frekvenci ma maximalni rozsah do 22 kHz, ale tam uz taky muze tezko kopirovat puvodni signal. Ke zkresleni taky dojde, ale myslim, ze je to za prahem rozliseni nas beznych posluchacu. Pokud si na aparature zapnete “ROCK”, “POP”, “HALL” a podobna nastaveni, zkreslite to daleko vic a dokonce to i poznate.
RE: RE: RE: RE: Digital vs. Zenit E
Ty seš mi nějakej zarytec. Všechno hodnotíš jenom podle tvých potřeb. Já koupil digiťák Olympuse C-4000 a ta potvůrka dělá přesně to, co jsem očekával. Potřebuji fotit např. u zákazníků rozmístění interiéru, ale žádné umělěcké foto. Čistě fakta pro dokumentaci. Pak to V PC stáhnu zpracuju a hotovo. Fotky vypálím na CD, vymažu kartu ve foťáku a tradá dál. Nedovedu si představit, že po každém focení budu jěště běhat nechávat vyvolávat fotky, které pak budu stejně skenovat a tištěné mi pak jsou k prdu. Tak co, i z thoto pohledu jsou digiťáky na ho..o ?
RE: RE: Digital vs. Zenit E
na filmi, a co fotky? Kupim digital a cvakam, cvakam, 250fotiek na 128Mb, 500 fotiek na 256Mb idem ku kompu a znova. zmazem, co sa mi nepaci…
no ale ty budes mat asi problem s PC.
Digital, digital
Aby som to zhrnul (ja som ten, co foti na Prakticu LTL-3). Digital povazujem za vhodny doplnok pre cloveka ktory chce fotit vela snimok prevazne reportazneho charakteru. Idealne napriklad pre reporterov. Na druhu stranu niekto ma s kinofilmom zlu skusenost (napr. aj taka znama firma, ako Kodak ma aspon na uzemi Slovenska minilaby, ktore vytvaraju humus, a nie fotografie – moj nazor). Kto chce, nech si kupi digital, ale na niektore veci, ako napriklad technicka fotografia to musi byt fakt dobry digitalny fotoaparat, aby sa mohol vyrovnat zrkadlovke.
Preco analog? To je rovnaka vec, ako napr. platna vs. CD, alebo elektronka vs. tranzistor. Taky elektronkovy zosilnovac ma meratelne omnoho vyssie skreslenie, ale na posluch hra prirodzenejsie – to potvrdi kazdy clovek, ktory sa len trochu vyzna do high-end techniky. O tom tu uz niekto zacal, ale toto nie je stranka o hudbe 🙂 Ja mam moznost tuto vec technicky posudit a ludom, ktori chcu pocuvat rozny umely akusticky shit (moj nazor, sorry ak som niekoho urazil), ako rozne techno a pod. odporucam CDcko. Na narocnejsiu hudbu… bohuzial. Toto uplne sedi aj pri digitale.
Dalsia vec, pre ktoru by som si digital nekupil (aspon nie na tento ucel) je isty nadych umenia plynuci z CB fotiek vlastnej vyroby. Toto dnes vacsina ludi vobec nechape, ale napriklad aj profesionali fotia na kvalitny digital a na CB fotky (akt, zatisie …) pouzivaju vyhradne film. Dovod je zrejmy na prvy pohlad, ked sa na taku fotku clovek pozrie. Vela ludi, ktori maju digital presli na \”cvakanie do prazdna\”. Nehovorim, ze by fotografie boli technicky zle (aj ked poznam aj take pripady), ale digital je vec vhodna pre reporterov, nie na zachytenie okamihu ocami vnimajucimi svet okolo seba (myslim naozaj vnimajucimi 🙂
Ako to skonci… Niekedy v buducnosti sa digitalne fotaky masovo rozsiria a film sa stane vysadou tych prachatejsich (S cb filmom by to bolo uz teraz, keby neexistovala stara dobra Foma). Potom si digital kupim aj ja – nie preto, ze by som chcel, ale preto ze nebudem mat inu moznost
RE: Digital, digital
hehe 🙂 ty si strasny komik, lepsi nez benny hill,
niezeby som bol extremnym nekritickym zastancom digitalnych technologii ale:
1) prd vies aky je rozdiel medzi elektronkou a tranzistorom (okrem toho ze si pocul ze elektronka produkuje ludskejsi? zvuk a je sklenena ze:)]
2) ad2 platna, je pravdou ze vzorkovacia frekvencia musi byt aspon 2x vyssia ako prehravana, t.j. zvuk na cd je orezany na 22KHz, ale platna je naozaj niekde uplne inde, je tam moznost teoreticky celeho frekvencneho spektra ale prakticky nemas tak jemnu mechaniku a tak ostru a presnu ihlu.
3) ak si videl pri praci niekedy skutocneho fotografa, ktory chce nejaky vysledok, tak ti je urcite jasne ze ma u seba nie jeden tesco film ktory si kupil za 49.90 v akcii, ale najmenej 5 slusnejsich filmov a z jednej sceny urobi aspon 3-4 castejsie aj viac fotografii [jedna fotosession s modelkou sa rata na stovky snimkov, z ktorych sa pouzije tak 1%]. jasne, co ty stlacis to je super, 36 snimkovy film mas vo fotaku 2 mesiace a velmi sa tesis ake super su tvoje zabery.
digital, digital
no ty taky pises o tom cemu tak uplne nerozumis, napr. existovala diskretni kvadrofonie na deskach, kde byly zadni kanaly modulovane na nadzvukove nosne a frekvencni rozsah tudiz sel dost pres 40kHz. takze mechanicky zaznam ma limity o dost vis nez se domnivas.
Pánové, už dost!!!
Pánové, buďte tak laskaví a svoje komentáře k tomuto článku pište pouze pokud se týkají tohoto článku. Nerozvíjejte zde dále debatu na téma, jestli je lepší digitál nebo klasika. Smiřte se s tím, že taková debata nemá jednoznačný závěr. Každému vyhovuje něco jiného, každý má jiné požadavky a každý je či není spokojen s tím co má. Zároveň taky každý něco chce a po něčem touží. Nemá proto žádný smysl tady argumentovat tím či oným, protože pro jiného takový argument nemusí být vůbec relevantní.
Na závěr – a opravdu bych rád, aby to tak skutečně bylo – přidávám jedno moudro od klasika české dokumentární fotografie Pavla Štechy z nedávné besedy: Je jedno, čím kdo fotí nebo co kdo fotí. Hlavně, že ho to baví a že z toho má dobrý pocit. A o to jde.
srovnani rozliseni filmu a CCD
Na tomhle linku je mozne si precist pomerne slusne provedene srovnani obou medii. Rozliseni ma obecne vliv nejenom na podani monochromatickych detailu, jak o tom byla rec v tomto dobre napsanem clanku, ale ovlivnuje i podani barev (mnozstvi zobrazitelnych barev). Proto srovnanim obou medii dojdeme pro obe kriteria k ruznym vysledkum.
http://www.users.qwest.net/~rnclark/scandetail.htm
Fotak s vyssim rozlisenim?
Bude tedy kvalitnejsi fotografie kdyz pouziji fotak s vetsim rozlisenim a potom udelam vyrez nebo interpoluji na mensi fotku?
cb
lze z toho clanku vyvodit,
ze u cb fotky se neinterpoluje?
d.
RE: cb
Pokud by slo o specialni sensor pro CB, pak by interpolace skutecne nebyla potreba. Nicmene u obycejneho digitalu, ktery ma funkce CB, sepie apod., se snima stejnym sensorem jako u barvy, s mozaikou barevnych filtru, a monochromaticky obraz se vyrabi dodatecne softwarove. Jelikoz sousedni bunky sensoru maji odlisnou spektralni citlivost, vystup nelze pouzit primo pro vytvoreni CB obrazu – je potreba kanaly dointerpolovat a teprve pak z nich zkombinovat CB obraz.
více barev
Nechám CB fotografii CB, ale naopak mě zajímá, jak a zda se změní rozlišení detailů, pokud se použije více barevný snímač. Např u sony F828 4barevný snímač.
Zajímalo by mě, zda se ta čtvrtá barva promítá různě do všech kanálů (nebo aspoň do dvou BG) a jaký to má vliv právě na rozlišení detailů. Algoritmus dostane navíc informaci o další barvě, může pak lépe vystihnout barvu bodu v RGB. To je asi bez problémů. Ale jak je to s těmi detaily.
Teoreticky mým prostým rozumem mi přijde, že dostane i jistou informaci o dalším různém místě od 4 snímače. Otázka je zda s tím algoritmus počítá. Zajímá mě prostě váš odborný názor.
btw:Nevím proč si nalhávat, že rozlišovací schopnost je oproti neiterpolovanému třetinová, když je jen o něco málo větší než čtvrtinová. Díky té zelené složce, ale defacto 25%.
RE: více barev
Kolik informace o dalsim miste kazdy z RGB kanalu ziska, zalezi na tom, jaka je barva ctvrteho pixelu. U Bayerova usporadani je barva ctvrteho pixelu zelena, tj. veskera informace jde do zeleneho kanalu. Pokud bude ctvrty kanal napr. achromaticky (citlivy na vsechny vlnove delky), tak maji sanci ziskat nejakou informaci vsechny tri kanaly, jenze zase vznika problem s tim, jak mezi ne namerenou hodnotu “rozpocitat”.(V tomto konkretnim pripade by se asi dalo vyuzit napr. nejakeho prostoru typu Lab a skutecnosti, ze lidske oko je citlivejsi na detaily v jasove slozce, zatimco v barevnych nepotrebuje tak velke rozliseni.) Ctvrty pixel v barve jednoho z kanalu a achromaticky (tj. kombinujici vsechny tri kanaly) jsou dva extremni pripady. Pouziti ctvrte barvy je nekde uprostred. Vysledek bude dost zalezet na pouzitem algoritmu (jehoz detaily bohuzel neznam), nicmene domnivam se, ze vylepseni bude spis jen marginalni – i se ctvrtou barvou je totiz potreba celkovy pocet vzorku nafouknout na trojnasobek. Navic to, ze individualni kanaly pri pouziti mozaikoveho sensoru maji diky nizsi hustote vzorku dane barvy nizsi rozliseni jen cast problemu. Problemy tu pusobi take to, ze mame informaci o ruznych barvach v ruznych bodech (a tudiz po dointerpolovani vznikaji barevne artefakty kolem hran objektu) – a to ta ctvrta barva take neodstrani. Tj. domnivam se, ze ctvrta barva ve spojeni s inteligentnim algoritmem muze trochu pomoci, ale zadne zazraky cekat nelze.
Ciara versus pixel
Ak som dobre cital, tak je tu porovnavana kresba objektivu napr.80car/mm a pocet pixelov u digi.
Ale snad plati ze 80 car je ekvivalent 160 pixelov,respektive na vykresleni 80 car potrebujem
160 pixelov.
Stan
RE: Ciara versus pixel
Jednoduse: ANO PROSIM, JO!
Stretnutie po rokoch
Neviem, ci ucastnici tejto zaujimavej diskusie si precitaju moj pripevok. Len vyuzijem heslo “Po vojne je kazdy generalom”..:))
Je rok 2006 a digitaly postupili milovymi krokmi dopredu. Je tu Mark D2 a zrazu je tu 16.7 Mpixelov. Ludia pouzivaju DSLR vo velkom a nedavno dokonca som zhanal v Kanade Nikon D200 pre mojho znameho. Bolo mi povedane, ze kludne mozem objednat a v aprili ho budem mat. Ja ze, tak dlho? Takze vraj preto, lebo na neho caka 16000 zaujemcov, tomu sa hovori mania.
Inac ten pretras digital versus film sa posunul nejak blizsie k digitalu (ved firmy ako Ilford, Kodak alebo Agfa hovoria za seba).
Ale na druhej strane sa prave pozeram na stenu, kde mam svoje fotografie. Pred rokom som fotil so svojim starym fotakom (ZENIT 212K, obj. Zenitar K2 50 2.0) na dnes uz problematicko vyvolavatelny film (vecna slava firme Agfa) Scala 200, inac ciernobiely diak. Potom som ho odskenoval na Nikon-e LS50 na 4000 DPI. Fotka ma rozmery 20×30, napriek tomu detaily a farebne tony su na nej fantasticke a ocividne to nebolo maximum (pre tlac som nepouzil cely rozsah suboru, rozmer bol 3600*2400 bodov, cize cca 2/3 rozlisenia). Ak by som chcel CB urobit v digitale samozrejme sa to da, len za to sa uz riadne plati. Na druhej strane moj postup je extrem. Lebo cena filmu + vyvolanie + poslanie (boli tri laby v Severnej Amerike, z toho jeden blizko mna, ktory zrusili) ma vysiel na 29 US, co za jeden film spolu s vybranymi obrazkami je uz palka.
Takze co v buducnosti? No snad najvacsie prsty drzim Pentaxu, od ktoreho mam vacsinu skiel a cakam na nejaku lepsiu DSLR, niekde na fore vraj niekdo napisal do Pentax-u a ti mu odpovedali, ze asi uvedu v roku 2006 nejaku 10 Mpix DSLR. Dufam, ze je to pravda.
P.S. Ako vestec odhadujem, ze Mr. Zenitarista uz asi presiel na digital…
Vyborny clanek
… skvely clanek, dlouho jsem nad timhle problemem premyslel, tento clanek mi to konecne objasnil … je videt, ze autorka ma matematicke vzdelani !!! … i laikovi musi byt jasne, ze pixel na monitoru obsahuje 3x vice informaci, nez pixel na snimaci, nevim jak by tyto chybejici informace chtel O Neff vykouzlit jinak nez interpolaci …
Skvělý článek
Začetl jsem se včera do diskuse, kde se probírala rozlišovací schopnost objektivů oproti současné generaci 10 MPx čipů DSLR. Vzpomněl jsem si na tento článek a asi potřetí si ho od začátku do konce přečetl…