Dejte mi prosím deset deka obrázku aneb jak se obrázky měří a váží

Ohledně měření velikosti digitálních obrázků panují značné zmatky. Centimetry, pixely, byty – co si vybrat? A všechno to ještě komplikuje jakási záhadná veličina, označovaná tajemnou zkratkou dpi. Pro řadu lidí je to jakási složitá magie, plná nezapamatovatelných formulek, se kterými si pořádně nevědí rady. Skutečnost je přitom ale jednoduchá. Pojďme se podívat věcem na zoubek.

V jednom z minulých dílů seriálu jsme si vysvětlili, že digitální obrázek není v zásadě nic jiného než dvojrozměrné pole – buď čísel (indexované a šedotónové obrázky) nebo trojic čísel (barevné obrázky). Každá položka pole reprezentuje jeden pixel, čili jeden bod obrázku. Jak se měří velikost dvojrozměrného pole? V centimetrech? V palcích? Ne! Jednoduše se specifikuje, kolik má řádků a sloupců. Základní mírou velikosti digitálního obrázku jsou proto jeho rozměry v pixelech. Počet řádků a počet sloupců. Zvykněte si měřit obrázky v pixelech. Centimetry sice mohou na první pohled vypadat přátelštěji, protože je používáme je od malička, dnes a denně, nicméně je to právě lpění na centimetrech, které dělá z měření digitálních obrázků galimatyáš.

Palce, centimetry a milimetry jsou dobré pro měření obrázků na papíře. Digitální obrázek ale není fyzický objekt a žádnou délku v centimetrech nemá. Pokud někdo hovoří o velikosti digitálního obrázku v centimetrech, říká tím buď „předloha, kterou jsem naskenoval, byla tak a tak veliká”, nebo „kdybych tenhle obrázek vytisknul, byl by tak a tak veliký”. Pokud přesně nevíme, jak obrázek naskenoval nebo jak by ho vytisknul, neřekne nám to o velikosti digitálního obrázku (t.j. o počtu pixelů) zhola nic. To jde sice napravit tím, že se uvede rovněž hustota vzorků (bodů) při skenování či tisku, nicméně tento způsob popisu velikosti obrázku je zbytečně komplikovaný a má jednu velmi zásadní vadu – není jednoznačný. Okamžitě se začneme zamotávat do toho, že například 24×36 mm při 4000 dpi (dpi znamená dots per inch, tzn. počet bodů na jeden palec), je totéž jako 32×46 cm při 300 dpi nebo zhruba 26,7×40 cm při 360 dpi. Jak je vidět na tomto příkladu, pokud se udává velikost tímto způsobem, je velmi obtížné na první pohled bez přepočítávání říct, jestli jsou dva obrázky stejně veliké nebo jestli je některý z nich větší a o kolik. Proto je lepší se tomu vyhnout. Budete-li se držet rozměrů obrázků v pixelech, pak tento problém mít nebudete.

Velikost digitálního obrázku

Známe-li velikost skenované předlohy a rozlišení skenu (t.j. hustotu bodů při skenování), snadno si velikost výsledného digitálního obrázku spočítáme. Vzhledem k tomu, že standartní jednotkou používanou pro rozlišení je dpi, čili počet bodů na palec, mají v tomto směru poněkud jednodušší život Američané a další zatvrzelé národy, které stále ještě vzdorují SI. Rozměry předlohy v palcích jednoduše vynásobí dpi a je to. Kdo dává přednost centimetrům, potřebuje vědět, že jeden palec je asi 2,54 cm. Abychom dostali počet bodů na jeden centimetr, musíme dpi vydělit 2,54. To znamená, pro velikost digitálního obrázku v pixelech pak máme

velikost digitálního obrázku v pixelech = velikost předlohy v cm x dpi / 2,54.

Podobně si můžeme snadno spočítat, jak bude při dané hustotě bodů velký vytisknutý obrázek. Pokud počet pixelů na šířku a na výšku vydělíme dpi, dostaneme velikost obrázku na papíře v palcích. To znamená, abychom dostali velikost v centimetrech, musíme ještě výsledek vynásobit koeficientem 2,54. T.j.,

velikost vytisknutého obrázku v cm = (velikost digitálního obrázku v pixelech / dpi) x 2,54.

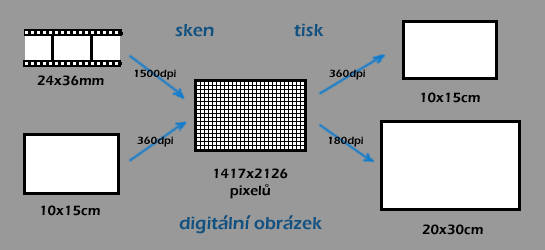
Nemáte rádi formulky? Nevadí. Je tu pro vás naše naprogramovaná kalkulačka pro počítání s dpi. Ne vždy je ale kalkulačka po ruce a tak vůbec není od věci si pamatovat třeba to, že políčko kinofilmu (24×36 mm) je zhruba 1×1,5 palce, takže při skenování kinofilmu je výsledný obrázek o něco málo menší než dpi x 1,5 dpi pixelů, t.j. např. při 2700 dpi to bude o trochu méně než 2700×4050. Podobně 10×15 cm je zhruba 4×6 palců, takže pri daném dpi potřebujeme pro standardní papírovou fotografii 10×15 cm přibližně 4 dpi x 6 dpi pixelů, pro fotografii 20×30 cm pak 8 dpi x 12 dpi pixelů atd. Tzn. budeme-li chtít tisknout např. při 360 dpi, budeme na fotografii 10×15 cm potřebovat digitální obrázek o rozměrech 1440×2160 pixelů. Budeme-li tisknout jen při 180 dpi, bude nám takováto digitální předloha stačit na fotku 20x30cm a na fotku 10×15 cm budeme potřebovat jen digitální obrázek o velkosti 720×1080 pixelů.

Jestliže měření digitálních obrázků v pixelech je obecně záhodné, pak při práci s obrázky, které nejsou určené pro tisk, ale pro monitor, je holou nezbytností. Ať už se jedná o obrázky, které chceme vystavit na webu, poslat někomu e-mailem nebo je třeba použijeme jako pozadí či screen saver. Velikost obrázku vždy musíme přizpůsobit rozlišení monitoru, na kterém bude zobrazován. To se udává také v pixelech. Standardně používaná rozlišení jsou 640×480, 800×600, 1024×768, 1280×1024 a 1600×1200 pixelů. Nejběžnější jsou ta uprostřed.

V praxi se běžně používají ještě další způsoby měření velikosti digitálních obrázků. Například u digitálních fotoaparátů jsou to také pixely, ale vžilo se udávat místo dvou čísel pro jednoduchost jen jedno – místo počtu sloupců a řádků se udává celkový počet pixelů (počet sloupců x počet řádků). A jelikož pixelů je požehnaně a vychází hausnumera, tak se výsledek vydělí miliónem a začne se mluvit o megapixelech.

Další přirozená míra velikosti digitálního obrázku, která je často užitečná, je objem dat v kilobytech nebo megabytech. Jsou možné dva různé způsoby specifikování objemu dat. Buď může jít o kombinaci informace o rozměrech obrázku v pixelech a bitové hloubce dat – např. 24-bitový barevný obrázek (pro každý pixel tři barvy po 8 bitech) o rozměrech 1024×768 pixelů představuje 3 byty krát 786 432 pixelů, t.j. celkem 2 359 296 bytů neboli 2,25 MB. Tento údaj nám může například pomoci si udělat představu, kolik paměti by náš počítač potřeboval mít, abychom s takovým obrázkem mohli pohodlně pracovat. Vzhledem k tomu, že také operační systém a pod. má jisté nároky a že budeme při úpravách pravděpodobně chtít přidávat k obrázku nové vrstvy a každý slušný editor si také drží starší verze obrázku, abychom mohli snadno odčinit škody, které jsme nechtě napáchali, tak je dobré mít paměti pokud možno i několikanásobně více, než jak velké jsou obrázky, se kterými hodláme pracovat. Ne že by s menším množstvím paměti tak velké obrázky zpracovávat nešlo, ale protože počítač pak musí nahrazovat nedostatek paměti tím, že si ukládá věci na disk a zase je odtamtuď načítá, což je mnohem pomalejší, než přístup k datům v paměti, je to velmi pomalé a upravování velkých obrázků ja pak velmi obtížné, protože počítač pak provádí naše akce s výrazným zpožděním, takže při úpravách kolikrát ani nevidíme, co děláme.

Tento způsob měření velikosti obrázku nám ale na druhou stranu neříká nic o tom, jak bude doopravdy veliký soubor, ve kterém bude obrázek uložen na disku. V předcházejícím dílu seriálu jsme se seznámili s formáty pro zápis obrázků a druhy komprese a kódování dat, které tyto formáty používají. Víme už, že velikost souboru může být značně rozdílná v závislosti jak na použitém formátu, tak na velikosti obrázku v pixelech a v neposlední řadě i na obrázku samotném. Obrázky, které obsahují málo náhlých přechodů a drobných textur se stlačují mnohem lépe. V řadě situací je proto praktičtější udat přímo velikost konkrétního souboru, ve kterém je obrázek uložen. Musíme mít ale na paměti, že pak sice víme, kolik nám obrázek zabere doopravdy místa na disku, nicméně to už neříká prakticky nic o tom, jaké jsou rozměry zakódovaného obrázku v pixelech. Proto není dobré udávat potřebnou velikost digitální předlohy pro tisk nebo pro zobrazení na monitoru prostřednictvím velikosti souboru v kilo nebo megabytech, jak to mnoho lidí s oblibou dělá. Je lepší zůstat u pixelů.

Příště si povíme něco o tom, co to vlastně znamená zvětšit nebo zmenšit digitální obrázek, jak se to provádí a jaké to má důsledky v praxi.