Měření a míchání barev

Úvod do CIE kolorimetrie a teorie míchání barev prostřednictvím aditivního skládání tří primárních barev a stručné shrnutí jejich důsledků při praktické reprodukci barev.

1. CIE XYZ systém měření barev

Potřeba vyjádřit barvy nějak čísly existovala již dávno před tím, než přišly na svět digitální obrázky. Možnost exaktně měřit barvy je totiž nezbytnou nutností při analýze jakéhokoli barevného materiálu, u něhož je přesnost barev kritická, včetně tradičních materiálů, jako je třeba barevný film nebo fotografický papír. O standardizaci kolorimetrických měření se již léta stará mezinárodní organizace zvaná Commission Internationale de l’Éclairage (CIE). Základním pilířem kolorimetrie je definice tzv. standardního kolorimetrického pozorovatele, kterou CIE vydalo v roce 1931.
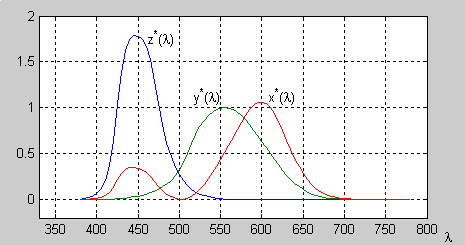
Standardní kolorimetrický pozorovatel CIE 1931 se skládá ze tří tzv. color matching funkcí, x^*(λ), y^*(λ) a z^*(λ). (Poznámka: V literatuře se pro color matching funkce normálně používají písmena s pruhem nad, nicméně tyto symboly se mi nepodařilo v HTML vyloudit, jelikož stávající browsery nejsou stále ještě plně kompatibilní s kódováním Unicode, takže jsem se v tomto textu uchýlila k menší odchylce od standardního značení.) Color matching funkce x^*(λ), y^*(λ) a z^*(λ) slouží ke stanovení speciální trojice čísel, tzv. XYZ tristimulu, který umožňuje navzájem porovnávat barvy různých barevných podnětů.

Obr. 1 – Color matching funkce x*(λ), y*(λ) a z*(λ) standardního kolorimetrického pozorovatele CIE 1931.

Barevný podnět je světlo vyzařované, odražené či propouštěné pozorovaným objektem, na které naše oči reagují (tj. díky kterému daný objekt vidíme). Toto světlo má jisté spektrální rozložení energie, které se dá popsat pomocí funkce f(λ), kde lambda je vlnová délka světla. Jednoduše řečeno, tato funkce udává, jak moc které vlnové délky je v tomto světle obsaženo. Spektrální rozložení energie podnětu, ačkoli určuje to, jakou barvu uvidíme, ovšem není samo o sobě dobrým prostředkem k charakterizaci a měření barev. Vztah mezi ním a viděnou barvou je pro tyto účely příliš složitý – viz minulý díl seriálu. Mimo jiné, protože je naše vidění pouze trojbarevné, tak se nám mnoho podnětů se zcela odlišnou spektrální distribucí energie jeví být zcela totožné barvy (metamerické podněty). Základní funkcí XYZ tristimulus je odstranění této nejednoznačnosti.

Standardní kolorimetrický pozorovatel byl zkonstruován tak, aby se dva podněty jevily být téže barvy, neboli byly metamerické, tehdy a jen tehdy, mají-li shodný XYZ tristimulus.

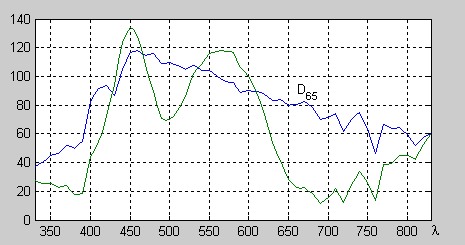
Obr. 2 – Spektrální distribuce standardního iluminantu CIE D65 modelujícího denní světlo při zatažené obloze a jednoho z jeho metamerů.

XYZ tristimulus je definován následovně:

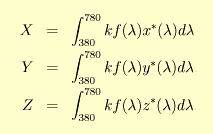
Zde k je kalibrační konstanta, jejíž hodnota záleží na tom, jaká je zvolená škála – lze používat i absolutní jednotky, ale nejběžnější je relativní škála v procentech, kde k se volí tak, aby hodnota Y byla rovna 100% pro dokonalý bílý difúzní reflektor, neboli matnou bílou plochu odrážející všechny vlnové délky stejně. (Pozor, to neznamená, že hodnota Y nemůže být vyšší než 100%. V praxi je potřeba počítat i s vyššími hodnotami, protože jasné odlesky, fluorescentní barvy apod. běžně dosahují hodnot přes 100%.)

Při použití XYZ tristimulu v praxi je potřeba mít na paměti, že jde pouze o sice na základě výsledků praktických měření odvozený, leč přece jen pouze teoretický model, jenž má svá omezení.

Z výše uvedené definice mimo jiné plyne, že se jedná o prostý lineární model, neboli se předpokládá, že:

1. XYZ tristimulus kombinovaného barevného podnětu se spektrální distribucí f(λ)+g(λ) je součtem tristimulů obou podnětů.

2. XYZ tristimulus podnětu zesíleného nebo zeslabeného jistým konstantnim faktorem, cf(λ) je prostým násobkem XYZ tristimulu původního podnětu f(λ) (stejným faktorem c).

Kromě toho je tento model např. i tranzitivní, neboli předpokládá i to, že jsou-li metamerické (čili vizuálně barevně zcela shodné) podněty f(λ) a g(λ), a stejně tak jsou metamerické i podněty g(λ) a h(λ), pak jsou nutně vzájemně metamerické i f(λ) a h(λ). Pokud jste si přečetli minulý díl seriálu, musí vám být jasné, že realita je mnohem komplikovanější a že takovýto jednoduchý model může platit jen přibližně (už např. jen proto, že vidění každého člověka se od průměrného standardního pozorovatele více či méně liší), jen v omezeném rozsahu situací (např. pouze pro jistý rozsah intenzit podnětů, velikost zorného úhlu, který porovnávané barevné plochy zabírají, apod.) a hlavně pouze jsou-li oba podněty pozorovány za zcela shodných pozorovacích podmínek (tj. je-li v obou případech zcela totožný stav akomodace zraku, identické okolí srovnávaných barevných ploch atd.).

Důležité je si též uvědomit, že XYZ tristimulus je čistě jen indikátorem shody barev – tj. mají-li dva podněty pozorované za týchž podmínek shodný nebo skoro shodný XYZ tristimulus, pak se (pochopitelně jen za okolností, kdy model s dostatečnou přesností platí) jeví být stejné nebo skoro stejné barvy:

Hodnota XYZ tristimulu ve skutečnosti neudává, jaká bude pozorovaná barva, tzn. neexistuje vzájemně jednoznačný vztah mezi jednotlivými barvami a hodnotami XYZ tristimulu – v závislosti na tom, jaké jsou pozorovací podmínky, stav adaptace našeho zraku atd. se nám totiž podnět s touž hodnotou XYZ tristimulu jeví být pokaždé poněkud jinak barevný.

2. Chromatické diagramy

V řadě situací je užitečné odhlédnout od intenzity příslušného podnětu, neboli ignorovat jas barvy a uvažovat jen její chromatičnost (barvu jako takovou – její „barevnost“). Toho je možné dosáhnout normalizací XYZ tristimulu. V kolorimetrii se tradičně používá jednoduchá normalizace

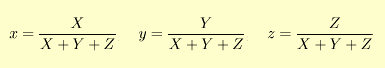
Pro tyto normalizované hodnoty tristimulu platí x + y + z = 1. Třetí hodnota je pak ovšem v takovém případě nadbytečná – lze ji snadno spočíst z předchozích dvou ( z = 1 – x – y ). Proto není potřeba ji uvádět a k zachycení chromatičnosti barvy stačí jen dvě hodnoty, x a y.

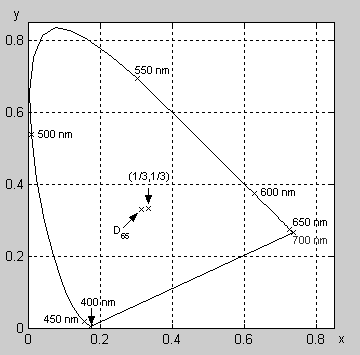
Obr. 3 – Chromatický diagram (CIE 1931) zachycující křivku čistých spektrálních barev.

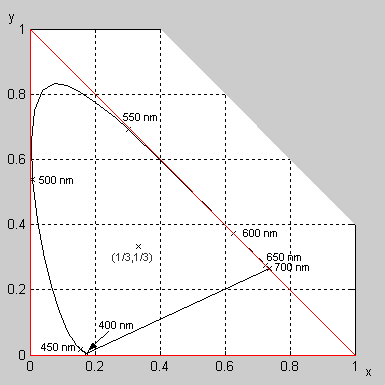
Redukce na pouhé dvě hodnoty umožňuje mimo jiné snadno znázornit řadu věcí graficky, prostřednictvím chromatických digramů, což jsou grafy, kde x se vynáší na vodorovnou a y na svislou osu. Příklad takového diagramu vidíme na Obr. 3. Křivka ve tvaru podkovy na diagramu zachycená se skládá z bodů (x_λ,y_λ), kde x_λ, y_λ jsou hodnoty chromatičnosti čistých spektrálních barev, tzn. barevných podnětů obsahujících jen jednu jedinou vlnovou délku světla, λ.

Bod (1/3,1/3) vyznačený na tomto diagramu odpovídá „bílé“. Přesněji, je to chromatičnost achromatického podnětu, který obsahuje všechny vlnové délky ve stejném množství („equal energy white“). Takovýto achromatický „bílý“ podnět se nám ovšem ve skutečnosti nejeví dokonale bílý – jakou barvu přesně uvidíme, závisí na pozorovacích podmínkách a stavu adaptace našeho zraku. Např. v denním světle, které se nám jeví být bílé, nejsou všechny vlnové délky zastoupeny rovnoměrně a chromatičnost denního světla je silně proměnlivá, v závislosti na denní době, počasí, apod. Je-li náš zrak adaptovaný na denní světlo, ve kterém převládají kratší vlnové délky (viz. spektrální distribuce standardního iluminantu D₆₅ modelujícího průměrné denní světlo při zatažené obloze na Obr 2.), tj. zdá-li se nám být takové světlo bílé, tak achromatický „bílý“ podnět, obsahující všechny vlnové délky ve stejném množství, se nám bude zdát ve srovnání s ním do oranžova.

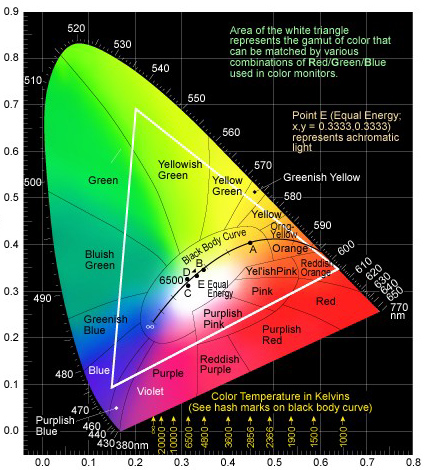
Obr. 4 – Barevný chromatický diagram (CIE 1931). Barvy jsou pouze přibližné, jednak protože podnět s touž chromaticitou se nám jeví pokaždé jinak v závislosti na pozorovacích podmínkách a jednak protože gamut monitoru, na který se díváte, je omezený – váš monitor nedokáže zobrazit všechny viditelné barvy.

Pro jednoduchost a názornost bývají chromatické diagramy často zobrazovány v barvách (viz Obr. 4) a mluví se o tom, že tento bod odpovídá červené a tamten zase modré. Pro vytvoření názorné představy je to velmi užitečné, je ale potřeba mít na paměti, že tato označení i barvy diagramu jsou jen přibližné a svým způsobem v některých situacích i trochu zavádějící. Stejně jako tomu je u XYZ tristimulu, chromatické souřadnice x a y jsou jen a jen indikátorem metamerické shody barev podnětů (v tomto případě jejich chromatičností), ale jejich hodnota neurčuje, jakou barvu přesně ve skutečnosti uvidíme. Ta totiž, jak už bylo řečeno, závisí kromě chromaticity daného podnětu i na dalších faktorech, konkrétně pozorovacích podmínkách a stavu adaptace zraku.

Chromatické diagramy mají jednu velmi pěknou vlastnost. Bod reprezentující chromatičnost světelného podnětu, který vznikne smícháním dvou světelných podnětů, kterým odpovídají body A a B v diagramu, leží na přímce spojující body A a B. Navíc, nejedná-li se čistě jen o teoretickou směs, ale takovou, která může v praxi skutečně existovat – což vylučuje použití záporných množství světla – pak takový bod leží mezi body A a B. Vzhledem k tomu, že každý reálně existující barevný podnět se skládá z nezáporných množství světla různých vlnových délek viditelného spektra, tak:

Všechny body, které odpovídají chromatičnosti reálně existujících světelných podnětů, jejichž barvu jsme doopravdy schopni vidět, leží uvnitř podkovy tvořené body odpovídajícími chromatičnosti čistých spektrálních barev.

Čára, která podkovu uzavírá a spojuje navzájem oba její konce, tzn. body odpovídající vlnovým délkám na obou koncích viditelného spektra – červeném a modrém – se sestává z bodů, které odpovídají směsím červené a modré a bývá nazývána fialová hranice.

3. Reprodukce barev aditivním mícháním tří primárních barev

3.1 Gamut primárních barev

Při reprodukci barev se používají tři zdroje primárních barev (nebo někdy i více), jejichž vzájemným mícháním se vytvářejí požadované barvy. Tři základní barvy jsou minimum, protože naše vidění je, jak už víme, trojbarevné. Spektrální rozložení energie podnětu, který je zapotřebí barevně reprodukovat, se přitom kompletně neduplikuje – jen se vytváří jiný podnět, který je s ním metamerický (neboli má stejnou barvu).

Na chromatickém diagramu leží body odpovídající barvám, které nevyžadují záporné množství některé z primárních barev a které tudíž potenciálně jde pomocí daných zdrojů primárních barev prakticky namíchat, uvnitř tzv. Mawellova trojúhelníka (je-li primárních barev více, řekněme n, tak n-úhelníka), který má vrcholy v bodech reprezentujících základní barvy k míchání použité. Na Obr. 5 je např. červenou barvou vyznačený Maxwellův trojúhelník pro standardní trojici základních barev definovanou CIE – čistou spektrální červenou o vlnové délce λ= 700 nm, zelenou λ= 546,1 nm a modrou λ= 435,8 nm. Zde jedna malá poznámka – Maxwellův trojúhelník je pouze teoretická aproximace reálného gamutu daných základních barev. V praxi totiž kromě záporných množství světla nelze přidávat ani neomezeně velká množství světla každé z barev. U reálného gamutu proto nejde ignorovat intenzitu a omezit se pouze na chromatičnost, je to tudíž trojrozměrný objekt, který má složitější tvar a nejde ho zredukovat do pouhých dvou dimenzí.

Vzhledem k tomu, že zdroje primárních barev použité při míchání reálně existují, body, které jim na chromatickém diagramu odpovídají, nemohou ležet mimo podkovu obsahující viditelné barvy. Tím pádem je ovšem celý Maxwellův trojuhelník vždy uvnitř podkovy. To ale znamená, že jisté části podkovy nevyhnutelně vždy leží mimo něj, a proto:

Ať už jsou v praxi primární barvy zvolené jakkoli, tak vždy existují barvy, které jsou mimo gamut zvolených primárních barev, tj. jde je z těchto primárních barev namíchat pouze teoreticky.

3.2 RGB systém

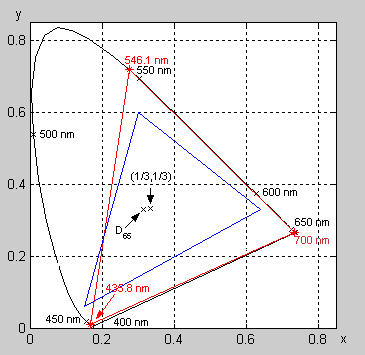
Podívejme na míchání barev pomocí tří primárních barev trochu blíže. Teoreticky tyto tři primární barvy mohou být jakékoli. Jediná podmínka je, aby byly nezávislé, resp. aby hodnoty jejich XYZ tristimulu byly nezávislé, tj. žádná z těchto trojic nebyla kombinací zbylých dvou a body, které těmto barvám odpovídají na chromatickém diagramu, tak neležely v jedné přímce a vytvářely trojúhelník. V praxi to zase tak úplně jedno není, protože tam je samozřejmě žádoucí, aby Maxwellův trojúhelník pokrýval pokud možno co největší část podkovy tvořené viditelnými barvami. Z tohoto důvodu se při aditivním míchání tří barev v praxi používají jako primární barvy červená, zelená a modrá, neboli tzv. RGB systém (R=red=červená, G=green=zelená a B=blue=modrá). Konkrétní přesná chromatičnost zvolených primárních barev bývá různá – RGB systém není jen jeden, ale je jich ve skutečnosti celá řada. Jak už bylo zmíněno, tak CIE standard třeba volí čistou spektrální červenou o vlnové délce λ=700 nm, zelenou λ=546,1 nm a modrou λ= 435,8 nm, s hodnotami chromatičnosti x_r=0,73, y_r=0,27, x_g=0,27, y_g=0,72 a x_b=0,17, y_b=0,01. Typický červený, zelený a modrý fosfor barevného CRT monitoru ale mají např. hodnoty chromatičnosti zhruba x_r=0,64, y_r=0,33, x_g=0,30, y_g=0,60, x_b=0,15, y_b=0,06, viz Obr. 5.

Obr. 5 – Srovnání Maxwellova trojúhelníka pro standardní CIE primární barvy (červeně) a typický červený, zelený a modrý fosfor barevného CRT monitoru (modře).

Nechť r(λ), g(λ) a b(λ), jsou funkce zachycující spektrální rozložení energie světla tří použitých zdrojů základních barev. Abychom z těchto tří základních barev namíchali barvu podnětu se spektrální distribucí f(λ), musíme najít trojici čísel R, G a B, takovou, že kombinovaný podnět se spektrální distribucí R r(λ)+G g(λ)+B b(λ) a podnět f(λ),
jehož barvu chceme namíchat, byly metamerické. Známe-li hodnoty XYZ tristimulu použitých primárních barev a barvy, kterou potřebujeme namíchat, pak lze hodnoty R, G a B spočíst ze vztahu

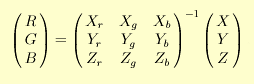
Z matematického hlediska je transformace XYZ tristimulu podnětu f(λ) na odpovídající RGB hodnoty lineární transformací, čili převedení hodnot XYZ tristimulu na RGB hodnoty můžeme chápat jako lineární změnu souřadnic v trojrozměrném prostoru barev.
V praxi je zvykem škálovat zdroje primárních barev r(λ), g(λ), b(λ) tak, že pro barevný podnět odpovídající ideálnímu bílému difúznímu reflektoru jsou hodnoty R, G a B shodné (100%).

Jiný způsob, jak nalézt hodnoty R, G a B je použít příslušné color matching funkce r^*(λ), g^*(λ) a b^*(λ). Základní vlastností těchto color matching funkcí je, že pro každou danou vlnovou délku viditelného spektra lambda je trojice RGB hodnot pro tuto čistou spektrální barvu rovna (r^*(λ),g^*(λ),b^*(λ)). Jinými slovy, tyto funkce jsou ideálním spektrálním rozložením citlivosti snímače vstupního zařízení, které snímá reálnou barevnou předlohu a produkuje RGB hodnoty, jako jsou skener nebo digitální fotoaparát. (Jako vždy, v praxi je to poněkud složitější, ale o tom si povíme jindy.) Pomocí color matching funkcí se RGB hodnoty podnětu f(λ), spočtou ze vztahu

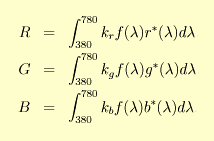
kde konstanty k_r, k_g a k_b se volí tak, aby výsledné hodnoty odpovídaly zvolenému škálování vzhledem k ideálnímu bílému difúznímu reflektoru.

Pro libovolnou trojici zdrojů primárních barev r(λ), g(λ), b(λ), příslušné color matching funkce jsou vždy lineárními kombinacemi color matching funkcí standardního kolorimetrického pozorovatele. Konkrétně,

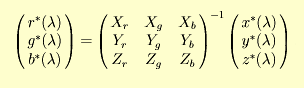
V praxi se udávají pouze hodnoty chromatičnosti primárních barev. Matice transformace se z nich sestrojí tak, že
se položí

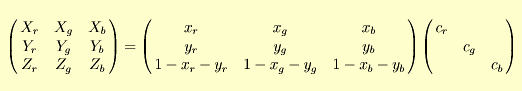
a konstanty c_r, c_g a c_b se doplní tak, aby transformace fungovala pro zvolené škálování XYZ tristimulu a RGB hodnot pro ideální bílý difúzní reflektor.

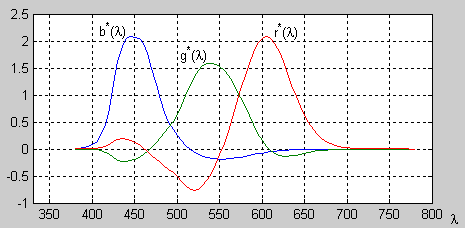
Obr. 6 – Color matching funkce pro typický červený, zelený a modrý fosfor barevného CRT monitoru.

4. Imaginární barvy

Bodům, které na chromatickém diagramu leží vně podkovy reálných, viditelných barev, se říká imaginární barvy. Ačkoli tyto barvy v praxi neexistují, z hlediska teorie jsou velmi užitečné.

Jak už bylo řečeno, barevné podněty produkované reálnými zdroji primárních barev nemohou obsahovat záporná množství světla některé z vlnových délek, neboli spektrální distribuce r(λ), g(λ) a b(λ) jsou nezáporné funkce. Na druhou stranu, některé barvy spektra jde namíchat z těchto primárních barev pouze teoreticky, protože leží mimo daný Maxwellův trojúhelník a vyžadují záporné množství některé z primárních barev, neboli jinými slovy color matching funkce r^*(λ), g^*(λ) a b^*(λ) nevyhnutelně nabývají i záporných hodnot.
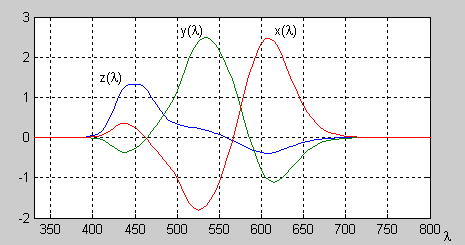
Funkce standardního kolorimetrického pozorovatele CIE 1931 x^*(λ), y^*(λ) a z^*(λ) si lze také představovat jako color matching funkce příslušející tří primárním barvám použitým pro míchání barev. Nicméně v tomto případě, protože funkce x^*(λ), y^*(λ) a z^*(λ) jsou nezáporné, spektrální charakteristiky hypotetických zdrojů primárních barev x(λ), y(λ) a z(λ) nutně musí být pro některé vlnové délky záporné (viz Obr. 7). To ovšem znamená, že takové zdroje v praxi nemohou existovat a jedná se pouze o imaginární barvy. Body, které takovým primárním barvám odpovídají na chromatickém diagramu, jsou mimo podkovu reálných, viditelných barev – konkrétně se jedná o body (1,0), (0,1), a (0,0). Všimněte si, že díky tomu, že hodnoty color matching funkcí standardního kolorimetrického pozorovatele CIE 1931 jsou nezáporné pro všechny vlnové délky lambda, hodnoty XYZ tristimulu jsou pro všechny reálné barevné podněty vždy nezáporné a celá podkova reálných, viditelných barev leží uvnitř Maxwellova trojúhelníka těchto imaginárních primárních barev s chromaticitou (1,0), (0,1), a (0,0), (viz Obr. 8).

Obr. 7 – Jedna z možných spektrálních distribucí imaginárních primárních barev x(λ), y(λ) a z(λ) pro color matching funkce standardního kolorimetrického pozorovatele CIE 1931.

Obr 8. – Podkova viditelných barev je na chromatickém diagramu CIE 1931 celá obsažena uvnitř trojúhelníka s vrcholy v bodech (1,0), (0,1) a (0,0).

Color matching funkce standardního kolorimetrického pozorovatele CIE 1931 byly ve skutečnosti odvozeny na základě praktických experimentů ve kterých měli pozorovatelé za úkol namíchat barvu, která jim byla promítnuta za pomoci zdrojů červeného, zeleného a modrého světla. Proč tedy CIE nezůstalo u RGB souřadnic a použilo jako základ svého standardu jiné, navíc ještě imaginární primární barvy? Jedním z důvodů je to, že pro reálné barvy, jak už víme, color matching funkce nabývají i záporných hodnot. Tím pádem by jednak tristimulus některých reálných barev nabýval záporných hodnot, což je trochu nepohodlné, ale hlavně nelze sestrojit přístroj na měření světla, jehož čidlo by mělo takovouto spektrální charakteristiku citlivosti. V dnešní době by nebyl problém toto obejít použitím čidel s jinou citlivostí a procesoru, který naměřené hodnoty příslušným způsobem přepočítá, nicméně v době, kdy standard vzniknul, byla situace poněkud jiná.
Kromě toho také byly imaginární primární barvy standardního kolorimetrického pozorovatele zvoleny tak, že color matching funkce y(λ) se shoduje se spektrální citlivostí standardního fotometrického pozorovatele, kterého CIE definovalo v roce 1924.
Tím pádem, hodnota Y v XYZ tristimulu současně vyjadřuje jas barvy, tak jak ho vnímá průměrný pozorovatel, a není třeba ho měřit zvlášť.

5. CIELUV a CIELAB sytémy měření rozdílů mezi barvami

Jak už zde bylo několikrát zdůrazněno, XYZ tristimulus je indikátorem metamerismu, neboli vizuální barevné shody (a to ještě jen za jistých standardních podmínek). Kromě toho, že hodnota XYZ tristimulu neříká, jak se nám bude barevný podnět přesně za daných podmínek jevit, tak stejně tak:

Ani absolutní rozdíl mezi hodnotami XYZ tristimulu (přesněji jejich vzájemná vzdálenost v trojrozměrném XYZ prostoru (∆X² +∆Y²+∆Z²)^1/2 ) nekoresponduje dost dobře s tím, jak moc se barvy od sebe vizuálně liší.

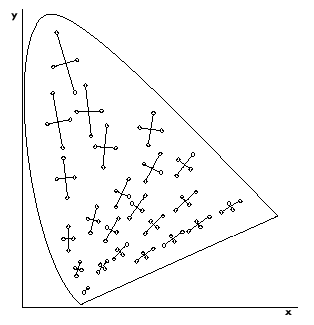
Na první pohled se může zdát, že jde o protiřečení si, ale není tomu tak. To, že podněty se stejnou nebo velmi blízkou hodnotou tristimulu vypadají stejně nebo hodně podobně, a ty, které mají tristimulus odlišný, zase jinak, totiž neříká celkem nic o tom v jakém přesně vztahu budou barvy, pro něž jsou hodnoty XYZ tristimulu výrazně odlišné. Naše vnímání rozdílů mezi barvami je vzhledem k souřadnicím XYZ nerovnoměrné, viz Obr. 9.

Obr. 9 – Relativní perceptuální rozdíly mezi barvami v chromatickém diagramu CIE 1931. Čáry spojují barvy, mezi kterými se člověku zdá být zhruba stejný rozdíl.

Vytvořit systém, který by umožňoval nějak přesně měřit vizuální rozdíly mezi barvami, je vysoce netriviální problém, který nebyl doposud zcela uspokojivě vyřešen. Kromě toho, že naše barevné vidění je velice komplikovaný proces, hlavní potíže při konstrukci takového systému spočívají v tom, že zatímco běžný pozorovatel je schopen poměrně přesně říct, kdy jsou pro něj dva barevné podněty vizuálně přesně shodné (což bylo zapotřebí k definování color matching funkcí), tak to, jestli rozdíl mezi těmito dvěma barvami je přesně stejně velký jako rozdíl mezi támhletěmi dvěma úplně jinými barvami, už tak snadno určit nedokáže. Navíc je to spíš už věc subjektivního názoru.

V běžné praxi se často pro měření rozdílů ve vzhledu barev používají dva standardní systémy, CIELUV a CIELAB. Oba jsou odvozené od CIE XYZ systému a jsou jeho nelineární transformací, která má za cíl zvýšit rovnoměrnost vzdáleností v tomto trojrozměrném barevném prostoru vzhledem k tomu, jak barvy doopravdy vnímáme, tj. zařídit, aby pokud možno vždy stejnému rozdílu mezi různými trojicemi hodnot odpovídajícími různým barvám, odpovídal velikostně zhruba stejný vizuální rozdíl mezi barvami, jak se jeví pozorovateli. Tyto standardní systémy jsou definovány následovně. X_n, Y_n a Z_n značí hodnoty XYZ tristimulu referenčního ideálního bílého difúzního reflektoru
(neboli XYZ tristimulus zvoleného osvětlení přeškálovaný tak, aby Y_n=100).

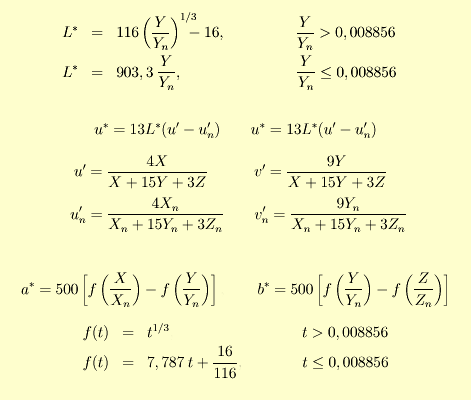
L^* je luminance, což je míra jasu barvy, vyjádřená v relativní škále v procentech vztažené k idálně bílému difúznímu reflektoru; u^*, v^* a a^*, b^* jsou chromatické souřadnice. V obou systémech se za míru absolutního rozdílu mezi dvěma barvami považuje prostá Eukleidovská norma rozdílu souřadnic ((∆L^*)²+(∆u^*)²+(∆v^*)²)^1/2, resp. ((∆L^*)²+(∆a^*)²+(∆b^*)²)^1/2 ). V obou systémech je také možné měřit rozdíl v barevném tónu dvou barev (bez ohledu na jas a saturaci). Jeho velikost je daná úhlem mezi spojnicemi bodů reprezentujících jednotlivé barvy a počátkem. V CIELUV systému je také možné snadno měřit rozdíly v saturaci barev (jejich barevné sytosti, pestrosti) – mírou saturace barvy je vzdálenost barvy od počátku v chromatickém diagramu se souřadnicemi u^*v^*, dělená luminancí. V CIELAB systému taková jednoduchá míra saturace barev neexistuje. Zato jsou ale chromatické souřadnice barevně intuitivnější – zatímco osa a^* je žlutomodrou osou, b^* představuje osu zeleno červenou.

6. Kolorimetrie a reprodukce barev v praxi

Barevné vidění člověka je příliš komplikované na to, aby bylo možné vytvořit praktický systém exaktního měření barev, tak jak je vidíme, který by fungoval stoprocentně a ve všech situacích. Existující kolorimetrické standardy poskytují nesmírně užitečný základ, bez kterého se nejde obejít, nicméně jsou založené na zjednodušených modelech a mají svá omezení, která je nutné mít v praxi na paměti. Například u obrazu v digitální formě nelze obvykle jednoduše jen změřit hodnoty XYZ tristimulu barevného podnětu na vstupu a později vyprodukovat výstup, který by měl stejnou hodnotu XYZ tristimulu, protože pozorovací podmínky se u snímaného podnětu na vstupu (např. reálné scény) často výrazně liší od podmínek, ve kterých typicky pozorujeme výslednou reprodukci (monitor, obrázek na papíře). Podněty se stejnými hodnotami XYZ tristimulu se nám pak jeví v obou případech jinak a reprodukce, která by prostě kopírovala hodnoty XYZ tristimulu, by se nám nezdála být barevně věrná. Kromě toho v řadě situací výstupní zařízení ani není schopné podnět s požadovanou hodnotou XYZ tristimulu vyprodukovat a je potřeba takovou hodnotu nahradit jinou, která dá barvu přijatelně blízkou. Proto v praxi nestačí pouze kolorimetrie, ale je zapotřebí vytvoření dodatečného systému správy barev, který vezme v úvahu typické pozorovací podmínky v různých situacích, jakož i základní vlastnosti lidského barevného vidění, charakteristiky vstupních a výstupních zařízení a v neposlední řadě i případná úmyslná vylepšení barev a na základě vhodně zvolených modelů provede transformace potřebné k tomu, aby se dosáhlo požadovaného vzhledu výstupu. O tom však víc až příště.